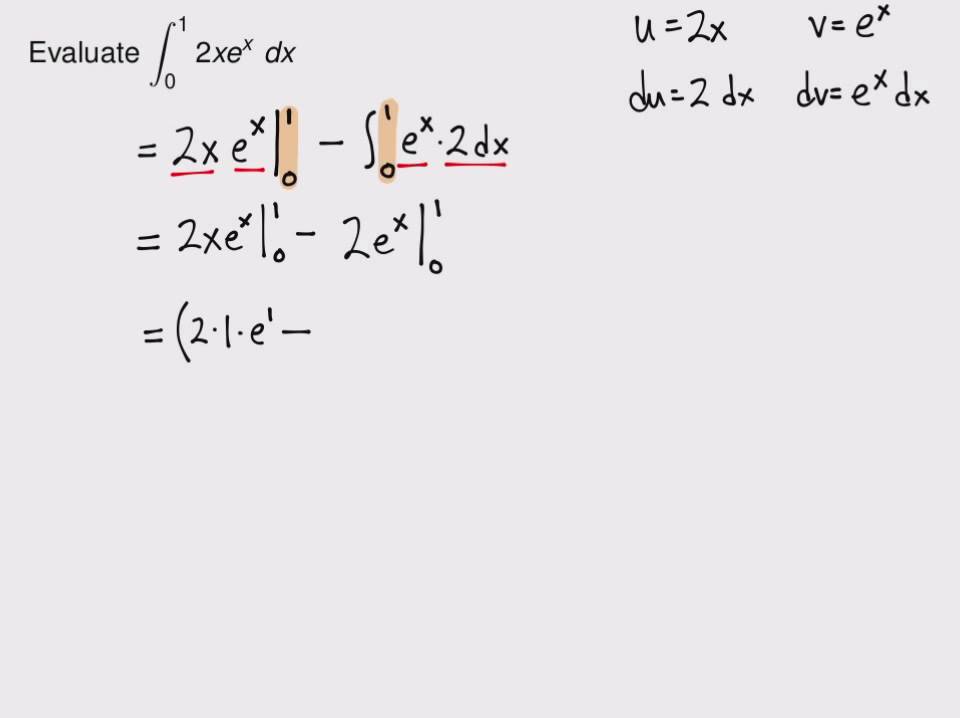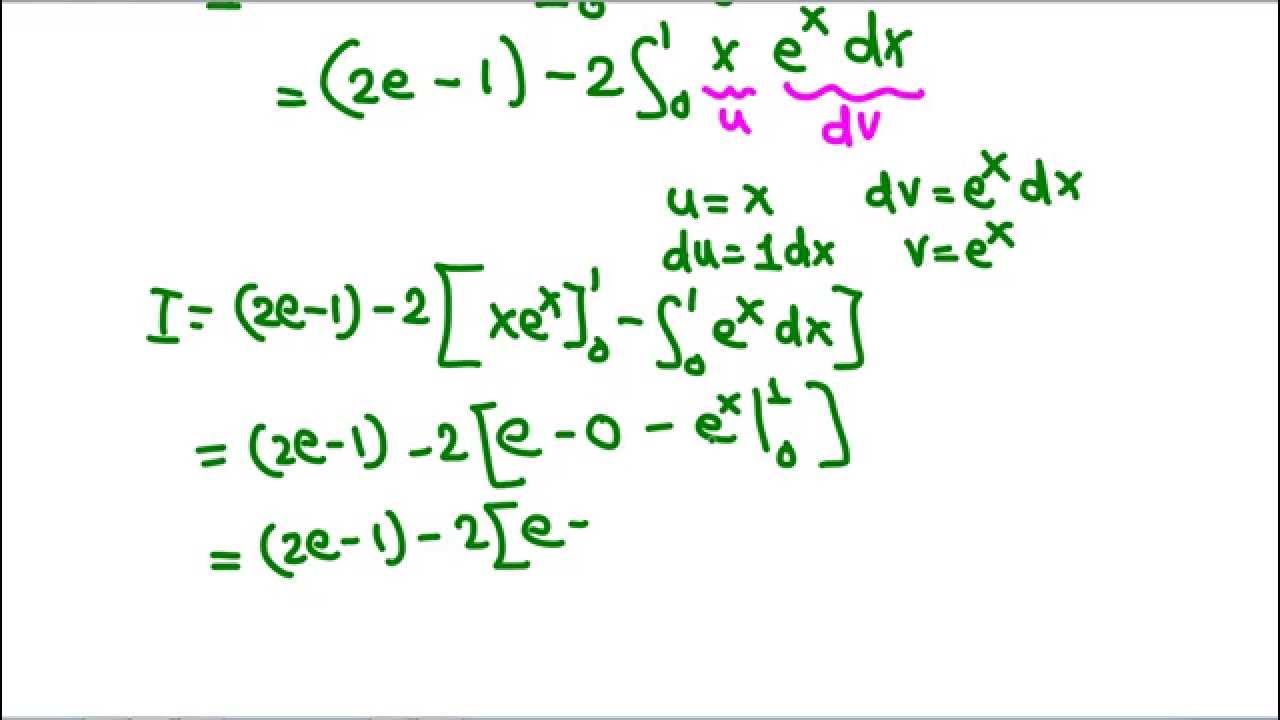∫ in ln (tan tan x) x dx. Evaluate the definite integral using integration by parts with way 2. D/dx [f (x)·g (x)] = f' (x)·g (x) + f (x)·g' (x) becomes.
Integration by Parts and Definite Integrals YouTube
Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways.
To solve this for p, we just add p to both sides:
Integration by parts is the inverse of the product rule for derivatives. We choose u = in ln (tan tan x) and dv = x dx. Integration by parts with a definite integral. U is the function u (x)
Thanks to all of you who support me on patreon.
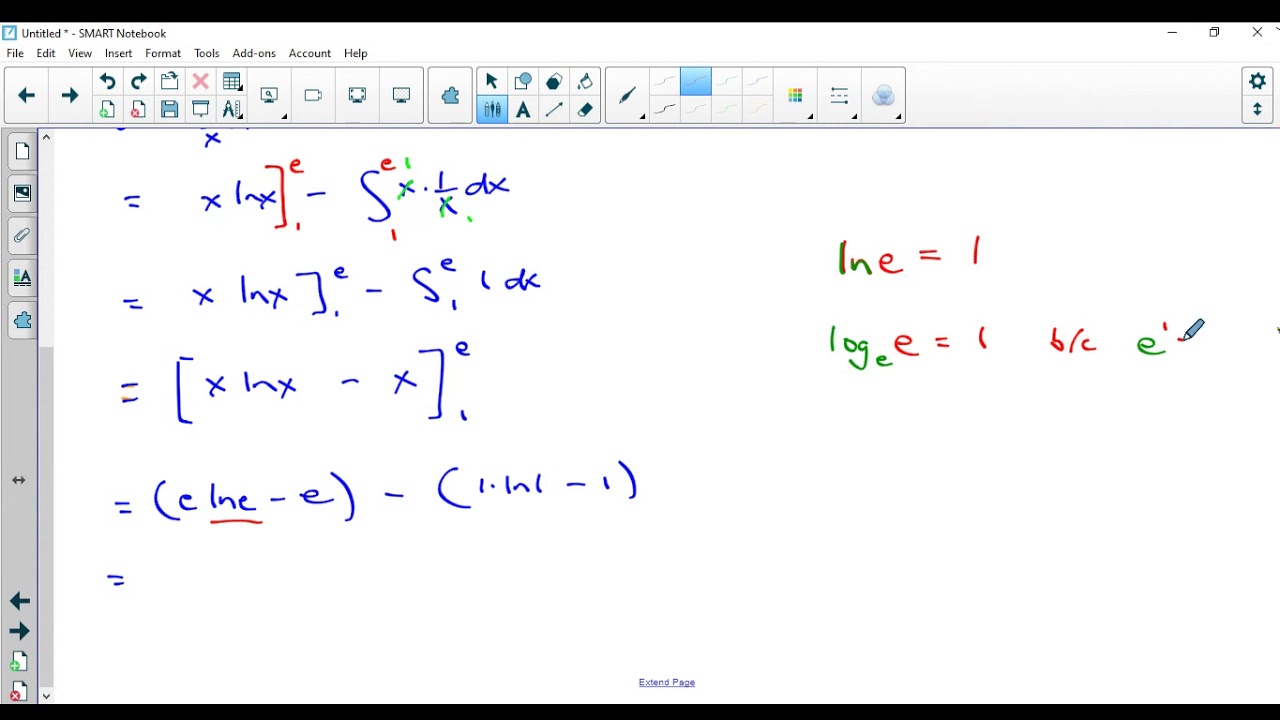
Previously, we found ∫ x ln. Try the free mathway calculator and problem solver below to practice various math topics. How to solve definite integration by parts. (1 week ago) integration by parts:
And practice evaluating double integrals by following examples.
Definite integration by parts is used when the function is a product of two terms of the independent variable. ( x) d x = x ln. We can integrate by parts on a definite integral, remembering to evaluate limits on each term. You will see plenty of examples soon, but first let us see the rule:
Evaluate definite integral limits using integration by parts with both rule 1 and 2.
Use the method of integration by parts to evaluate the definite integral {eq}\int_0^4 xe^x\ dx {/eq}. This article talks about the development of integration by parts: Consider the the following example: (fg)' = f'g + fg'.
Approximating a definite integral using rectangles 4:
Is the family of all antiderivatives of xe x, we can get one particular antiderivative by taking c = 0. ( x) d x, it is probably easiest to compute the antiderivative ∫ x ln. X − 1 4 x 2 + c. We see that it makes sense to choose u = 3x and dv dx = sinx it follows that du dx = 3 and v = z sinxdx = −cosx (when integrating dv dx to find v there is no need to include a constant of integration.
Math ap®︎/college calculus bc integration and accumulation of change using integration by parts.
P = (− q + r )/2. Integration by parts uv formula. Simpson's rule to approximate a definite integral 6: Solution compare the required integral with the formula for integration by parts:
As derived above, integration by parts uv formula is:
The u and v terms are decided by liate rule. One term is called as u and another term is called as v. Definite integration by parts is similar to integration by parts of indefinite integrals. Using same procedure, make f(x) = t.
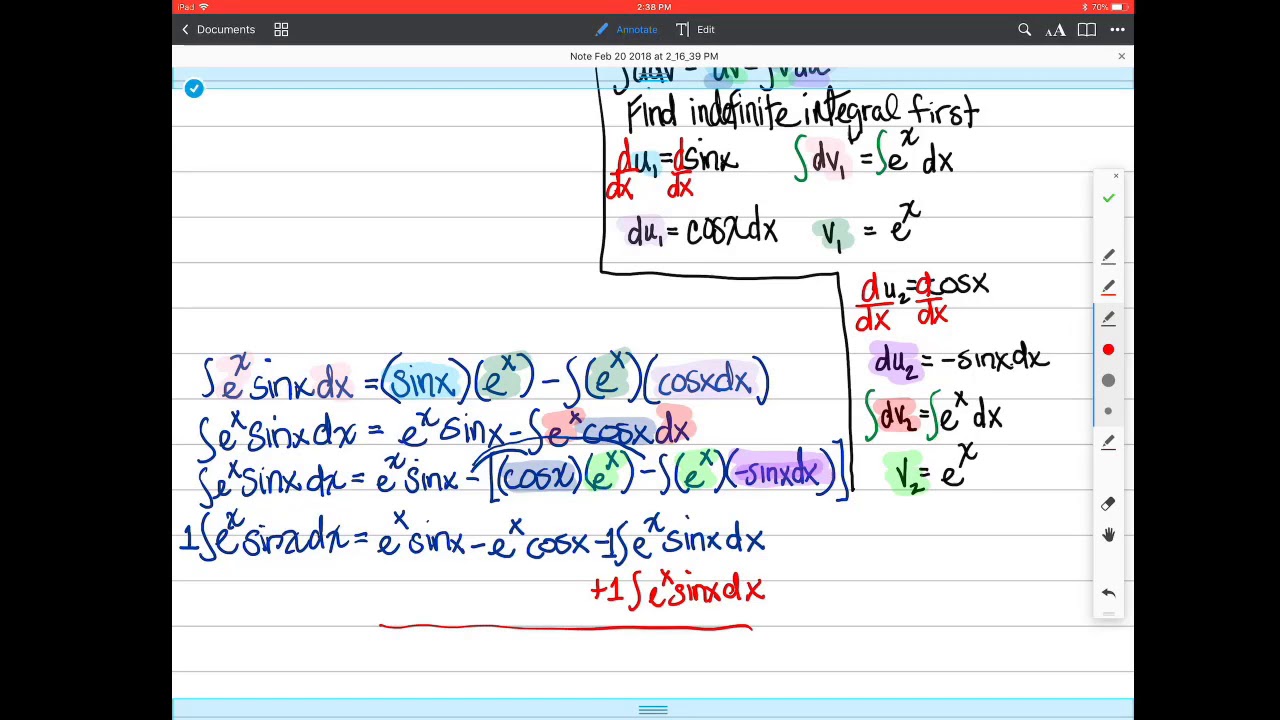
First we integrate the corresponding indefinite integral using integration by parts.
Dividing both sides by 2 gives: Try the given examples, or. Clear example of integrating xcos2x between 0 and π/4 \int _ { 1 } ^ { 2 } x.lnx dx solution:
∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u.
Integration by parts, definite integrals. This one a bit deeper: For solving the above definite integral problem with integration by parts using rule 1, we have to apply limits after the end of our result 2 p = −q + r.
Then divide both sides by 2:
∫ u v dx = u ∫ v dx − ∫ u' ( ∫ v dx) dx. Trapezoidal rule to approximate a definite integral 5: Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point. Definite integrals (practice) | khan academy.
I add to both sides:
So we have solved equation [5] for , giving us the desired result. So we will do the same to our integral equation, number [5]. ← video lecture 19 of 60 →. P = − q + r − p.
Same deal with this short form notation for integration by parts.
Then we can use the resulting antiderivative. Evaluating definite integrals using integration by parts:
