The effect of this change will give the order of the reaction with respect to b. The table also gives the meaning of the slope and intercept when these graphs. The integrated rate law can be rearranged to a standard linear equation format:
Graphical forms of integrated rate laws YouTube
In this case, we can say that [a]= [b], and the rate law simplifies to:
For the reaction where some reactant, r, goes to products (i.
Concentration at any moment of time can be given as, [a] = [ a] 0 e − k t. Ln[ ]=− g p+ln[ ]0 The units are calculated by the following equation: More generally speaking, the units for the rate constant for a reaction of order (m + n) ( m + n) are mol1 − (m + n)l(m + n) − 1s−1 mol 1 − ( m + n) l ( m + n) − 1 s − 1.
N order reactions rate = k[a] n
Chem 142 experimen t #5: These equations can be used to calculate, based on reaction order and the rate constant (which is temperature dependent) integrated rate laws L mol −1 s −1 • evaluate absorbance versus time measurements to determine the order of a reaction.
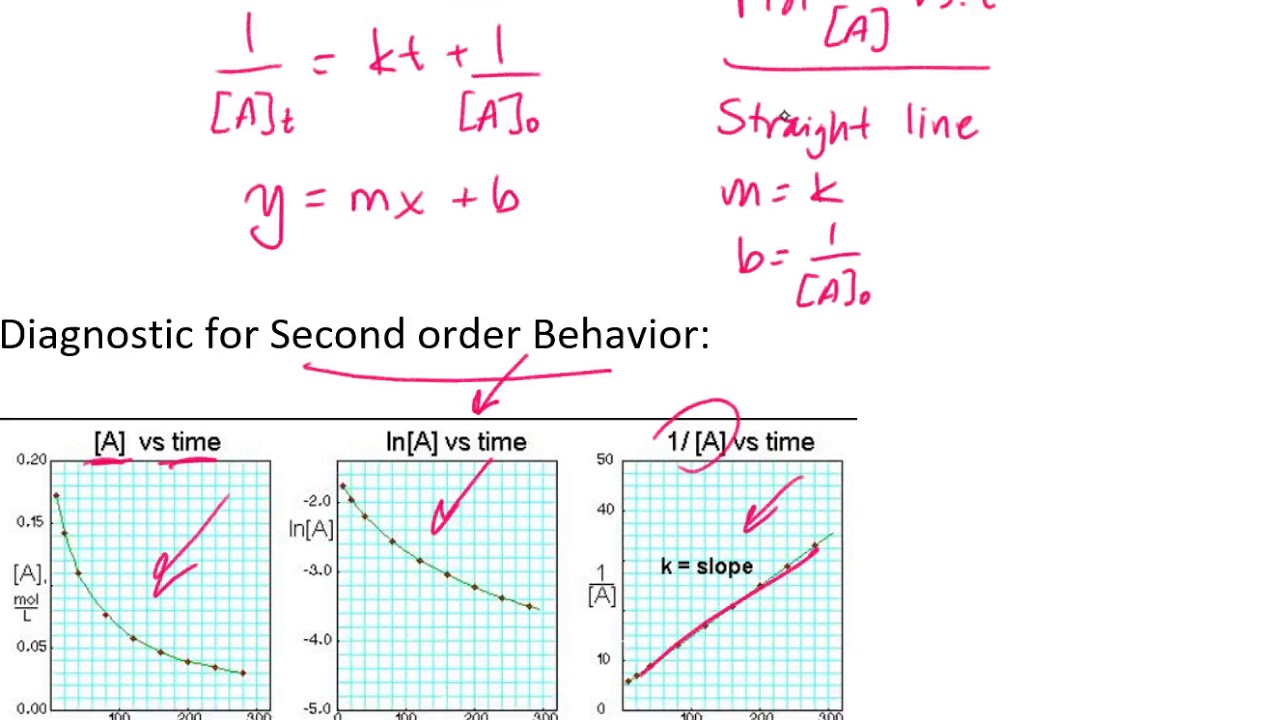
2a products or a + b products (when [a] = [b]) , rate = k[a] 2 the integrated rate law is 1/[a] = kt + 1/[a o ]
Since rate constant is given by rate = k [ a] x [ b] y. The first is that the initial concentrations of a and b are equal, which simplifies things greatly. Kinetics i (integrated rate law) goals of this lab: It explains how to use the integrated rate laws for a zero order, first.
Mol l −1 s −1:
The concentration is represented in mol l − 1 or m and time is represented in seconds. Reaction order integrated rate law characteristic kinetic plot slope of kinetic plot units of rate constant; Following the mathematical approach of previous examples, the slope of the linear data plot (for decomposition on w) is estimated from the graph. \ (\frac {1} {\left [a\right]}\phantom {\rule {0.1em} {0ex}}=kt+\phantom {\rule {0.2em} {0ex}}\frac {1} { {\left [a\right]}_ {0}}\) where the terms in the equation have their usual meanings as defined earlier.
Zero [e] t = −kt + [e] 0 [e] vs.
• create and use a calibration curve for the absorbance/concentration relationship for crystal violet. Then the [b] is changed, but is still present in excess. Third order reactions rate = k[a] 3 rate = k[a] 2 [b] rate = k[a][b][c] m/t = k m 3 k units: Ln [a] t = −kt + ln [a] 0:
Where, [r 0] is the initial concentration of the reactant (when t = 0) [r] is the concentration of the reactant at time ‘t’ k is the rate constant;
First order reactions rate = k[a] m/t = k m k units: Rate = k[ala [b]b but since [b] doesn't really change, this becomes rate = where k' = k[b] the results can then be analyzed using the integrated rate laws. [a] = − kt + [a]0 y = mx + b. = 5.00 m 0.100 0.098 0.096 0.094 0.092 0.090 0.088 0.086
Rate = k[a]2 r a t e = k [ a] 2.
On the other hand, integrated rate laws express the reaction rate as a function of the initial concentration and a measured (actual) concentration of one or more reactants after a specific amount of time (t) has passed; K = ( m ⋅ s − 1) × ( m − n) = m ( 1 − n) ⋅ s − 1. This chemistry video tutorial provides a basic introduction into chemical kinetics. • analyze graphs of data to determine best linear fit.
Rate = k[a] 0 m/t = k k units:
E., r products), the rate law is given by the expression: Rate = k[a]0 = k. The equation for the reaction is shown here. [a] −kt + [a]0 y.
If [ a] = [ b] then, [ a] x + y where x + y = n.
Table 7 summarizes the rate constant units for common reaction orders. Table 17.1 integrated rate law summary; Second order reactions rate = k[a] 2 rate = k[a][b] m/t = k m 2 k units: Thus, we can determine the concentration and rate of reaction at any moment with the help of integrated rate equation for zero and first order reaction.
Rate = k[a]0 = k rate = k [ a] 0 = k.
Rate = = k [a] calculus can used to integrate this expression to give us a useful equation relating the rate constant, k, with [a] 0, the initial concentration, and [a] t, the concentration after time, t, has passed. R a t e = k [ a] n. So, k = r a t e [ a] x [ b] y. Rate = k [r] n.the table below shows how to graph the data of [r] as a function of time, [r] t, for each of the possible overall orders of the reaction (n).).