To know and be able to apply the integrated rate laws for zeroth, first, and second order rate laws. Rate = k[a] rate = k[a] 2: Determining rate law from time and concentration data.
AP Chemistry Notes 6.5 Integrated Rate Laws Basics YouTube
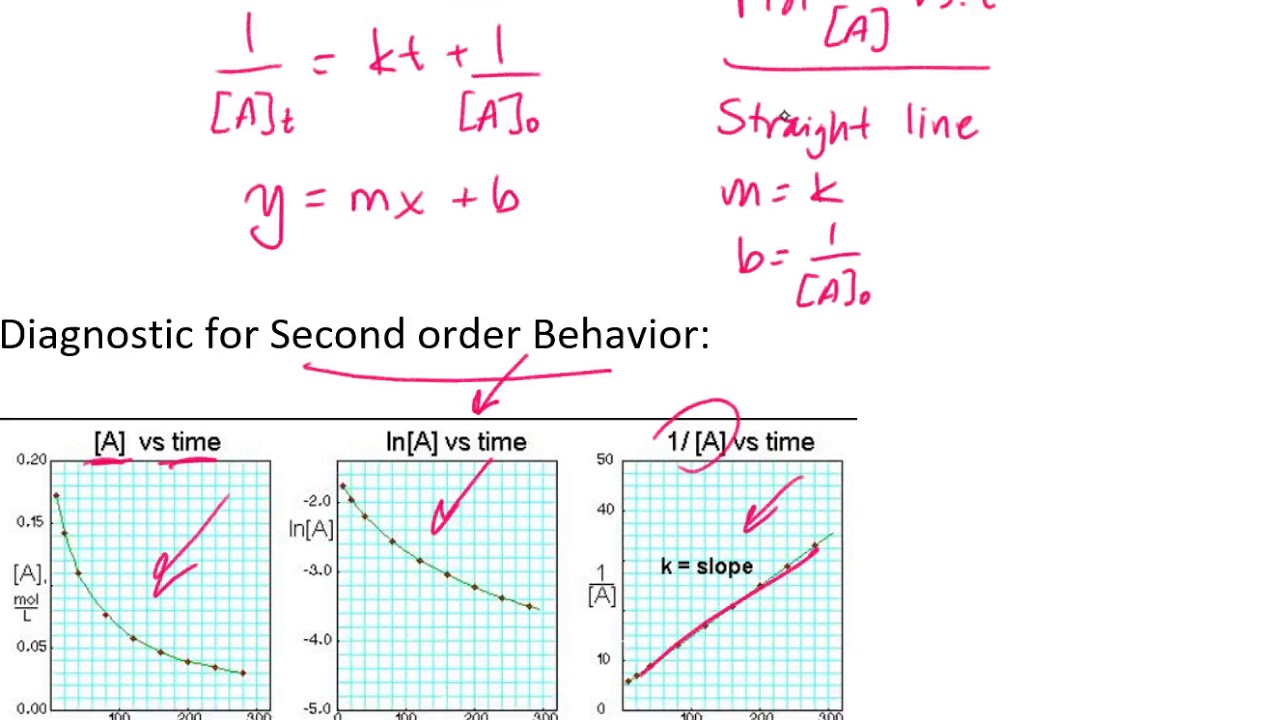
1 [ a] = kt + 1 [ a]0 y = mx + b.
The primary purpose of the integrated rate laws is that they allow us to calculate concentration changes over time.
Each equation is specific to its order so the order of a reactant must be known before one can calculate its change in concentration over time. This problem can easily be solved by calculating how far the car. For the reaction where some reactant, r, goes to products (i. Following the mathematical approach of previous examples, the slope of the linear data plot (for decomposition on w) is estimated from the graph.
No 2 + co no + co 2.
Using the integrated rate law expressions, we can find the concentration of a reaction or product present after sometime in the reaction. [ a] t = − k t + [ a] 0 y = m x + b. E., r products), the rate law is given by the expression: For reactions of the form aa → products and follow the general rate law rate = k[a]n.
The sum of the exponents (a+b+c+…) is the order of the reaction.
Where, [r 0] is the initial concentration of the reactant (when t = 0) [r] is the concentration of the reactant at time ‘t’ k is the rate constant; Where the exponents, a,b,c,…, may be zero, integers or fractions. [a], [a] 0, k, and t. This chemistry video tutorial provides a basic introduction into chemical kinetics.
[no 2] at 2.7 x 104 s after the start of the rxn
Ln[a] = −kt + ln[a] 0 \(\dfrac{1}{[a]}=kt+\left(\dfrac{1}{[a]_0}\right)\) Order with respect to no 2: These are inherently differential equations, because the rate is always defined as a change in concentration with time; A review | constants periodic table learning goal:
The table also gives the meaning of the slope and intercept when these graphs are.
For a zero order reaction: Zeroth order (n = 0): The rate of this rxn depends only on no 2: The following data were collected.
It explains how to use the integrated rate laws for a zero order, first.
At time, t=0, [a] = [ a] 0. The table below shows how to graph the data of [r] as a function of time, [r]t, for each of the possible overall orders of the reaction (n). (use the integrated rate laws and graphing to get orders). The integrated rate law can be rearranged to a standard linear equation format:
As long as three are know the fourth can be calculated.
Integrated rate law [a] = −kt + [a] 0: The rate law calculator has rate of reaction functions for zero order, first order and second order reactions as follows: What mile marker will the car reach after 2 hours? The above equation is known as integrated rate equation for zero order reactions.
1 [ a] = k t + 1 [ a] 0 y = m x + b.
These rate laws help us determine the overall mechanism of reaction (or process) by which the reactants turn into products. The order of the reaction is “n”. In this section, we will look at the integration of 1st, 2nd and 0th order reactions and some interesting graphs that. 𝑅 p =− [ ] = g[ ] on the other hand, integrated rate laws express the reaction rate as a function of the initial concentration and a measured (actual) concentration of one or more reactants after a specific amount of time (t) has passed;
Rate law for this reaction:
2a products or a + b products (when [a] = [b]) , rate = k[a] 2 the integrated rate law is 1/[a] = kt + 1/[a o] top The differential rate law can be integrated with time to describe the change in concentration of reactants with respect to time. To understand how to use integrated rate laws to solve for concentration a car starts at mile marker 145 on a highway and drives at 55 mi/hr in the direction of decreasing marker numbers. We can see that for a zeroth order reaction a plot of [a] vs t will give a straight line, with the.
Rate = k [a]a [b]b [c]c.
Zero order rate law (integral form) zero order half life zero order rate law first order rate law (integral form) first order half life first order rate law second order rate law (integral form) second order half life second order rate law the science. Putting the limits in equation (1) we get the value of c, ⇒ [ a] 0 = c.