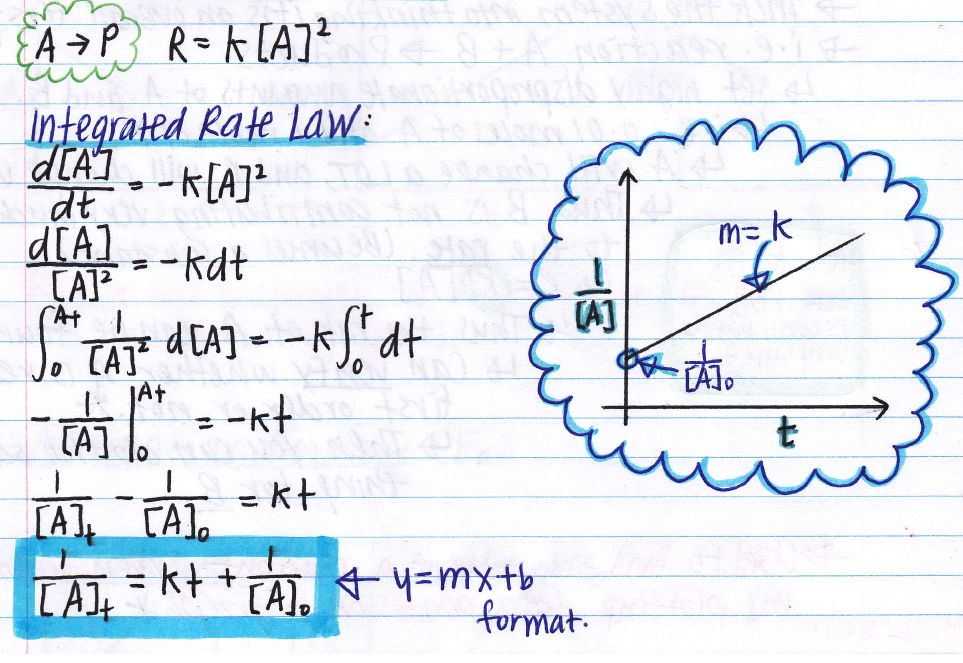
Integrated rate law [a] = −kt + [a] 0: The integral form of the equation was obtained from the differential form and the full integration can be found here. − d [ r] d t = k [ r] 2.
Rate Constant Equation Second Order Tessshebaylo
Rate = k[a] rate = k[a] 2:
The second order integrated rate law is {eq}1/[a]_t = kt + 1/[a]_0 {/eq}.
𝑅 p =− [𝑨] 𝒕 = [𝑨] we separate the variables and integrate over the interval: Y as a function of time yields a line for [a] that is equal to k. ∫ [ ] [ ]2 [𝐴] [𝐴]0 =− g∫ 𝑡 𝑡0 recall from calculus that (or check a table of integrals): This curve is defined based on slope of the line, which is.
Considering the scenario where one second order reactant forms a given product in a chemical reaction, the differential rate law equation can be written as follows:
Because this equation has the form y = mx + b, a plot of the inverse of [a] as a function of time yields a straight line. In mathematical language, these are first order differential equations because they contain the first derivative and no higher derivatives. The rate law calculator has rate of reaction functions for zero order, first order and second order reactions as follows: The rate constant for the reaction can be determined from the slope of the line, which is equal to k.
Because this equation has the form y = mx + b, a plot of the natural log of [a] as a function of time yields a straight line.
Look carefully, and you'll notice that the equation for the second order integrated rate law is in the form y = mx +b, where y = 1/a; A chemist calls them second order rate laws because the rate is proportional to the product of two concentrations. −d[r] /dt = k[r] 2; By elementary integration of these differential equations integrated rate laws can be obtained:
2a products or a + b products (when [a] = [b]) , rate = k[a] 2 the integrated rate law is 1/[a] = kt + 1/[a o ]
1 [ a ] vs. Ln[a] = −kt + ln[a] 0 \(\frac{1}{\left[a\right]}\phantom{\rule{0.1em}{0ex}}=kt+\left(\frac{1}{{\left[a\right]}_{0}}\right)\) plot needed for linear fit of rate data [a] vs. Second order reactions ( j=2) the differential form of the rate law is: How to calculate second order rate constant from graph?
Using the integrated rate law, two products are merged with 1/ [a]_t = 1/ [a]_0 in the event that the last second has no effect.
Rate = k[a] rate = k[a] 2: Using the integrated rate law expressions, we can find the concentration of a reaction or product present after sometime in the reaction. (1) where, c= constant of integration, at time, t=0, [a] = [ a] 0. These are inherently differential equations, because the rate is always defined as a change in concentration with time;
If the plot is not a straight line, then the reaction is not second order.
1 [ a ] = k t + ( 1 [ a ] 0 ) 1 [ a ] = k t + ( 1 [ a ] 0 ) plot needed for linear fit of rate data [a] vs. Putting the limits in equation (1) we get the value of c, ⇒ [ a] 0 = c. Written by noah january 27, 2022. Integrated rate law [ a ] = − k t + [ a ] 0 [ a ] = − k t + [ a ] 0.
In this section, we will look at the integration of 1st, 2nd and 0th order reactions and some interesting graphs that.
Zero order rate law (integral form) zero order half life zero order rate law first order rate law (integral form) first order half life first order rate law second order rate law (integral form) second order half life second order rate law the science. In order to obtain the integrated rate equation, this differential form must be rearranged as follows: The differential rate law can be integrated with time to describe the change in concentration of reactants with respect to time.