Thus, the graph of the second order integrated rate law is a straight. \ [\dfrac {1} { [\mathrm {a}]_t} = kt + \dfrac {1} { [\mathrm {a}]_0}\] see handout on how to transform and. These are inherently differential equations, because the rate is always defined as a change in concentration with time;
Principles of Chem 2
So this is our integrated rate law.
Using the data for t = 0s and t = 6200 s, the rate constant is estimated as follows:
Some people call this the integrated rate equation. Therefore, the rate law for this reaction is, We can arrange this to get the integrated rate law: This is exactly what's expected, as this is the maximum value of the rate of product formation.
∫ [ ] [ ]2 [𝐴] [𝐴]0 =− g∫ 𝑡 𝑡0 recall from calculus that (or check a table of integrals):
The equation for the second order integrated rate law takes the form y = mx +b, where y = 1/a; The rate of reaction is given as shown below. So we plug in this first. Where, k is the first order rate constant where, k is the first order rate constant integrate the above equation (i) between the limits of time t = 0 and time equal to t, while the concentration varies from initial concentration [a 0 ] to [a] at the later time.
Conflating the 2 inside the constant for the first, derivative, form will only make it required in the second, integrated form (presented below).
So we found our integrated rate law for a second order reaction. 𝑅 p =− [𝑨] 𝒕 = [𝑨] we separate the variables and integrate over the interval: Ln( a(b −x) b(a −x)) = (b −a)kt. Consider the reaction r → p again.
Ln([a]0[b] [b]0[a]) = ([b]0 − [a]0)kt.
In terms of the original symbols, the rate law becomes. So we have one over the concentration of [a]t minus one over the initial concentration of a, and then on the right side, this of course would just be kt. Aa + bbc (1) the rate of reaction (1) is given by: Rate = k[nh 3] 0 = k.
A second order rate law means that the rate of reaction depends on the concentration of two reactants raised to the first reaction, or one reaction raised to the second power.
By elementary integration of these differential equations integrated rate laws can be obtained: In mathematical language, these are first order differential equations because they contain the first derivative and no higher derivatives. Your equation gives d x d t = k [ a] 0 [ b] 0. Rate law can be expressed as, rate = k [a] 1.
Second order reactions ( j=2) the differential form of the rate law is:
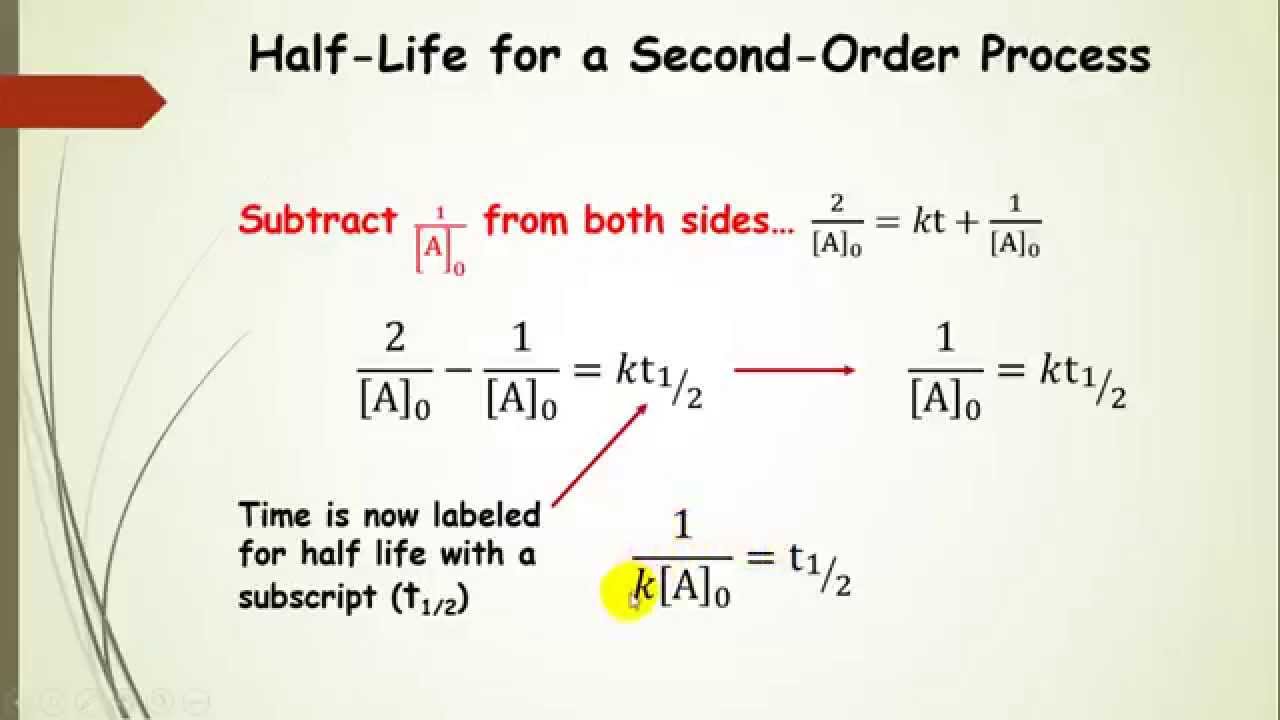
1 revisiting integrated rate law derivation. Plot the concentrations of a, b, and as a function of time. 2nd order reaction integrated rate law 1 [𝐴𝐴] = 𝑘𝑘 +𝑑𝑑1 [𝐴𝐴]0 at time t = t1/2 [𝐴𝐴] = 1 2 [𝐴𝐴]0 therefore 1 [𝐴𝐴] = 2 ∙1 [𝐴𝐴]0 substitute for [a] 2 ∙1 [𝐴𝐴0] = 𝑘𝑘𝑑𝑑1⁄2+ 1 [𝐴𝐴]0 rearrange the terms 2 ∙1 [𝐴𝐴0] − 1 [𝐴𝐴0] = 𝑘𝑘𝑑𝑑1⁄2 1 [𝐴𝐴0] Then the reaction is done when x = [ a] 0.
The graph of the reaction rate with respect to initial concentration shows that it is an exponential function such that the rate increases by the square of the concentration of the reaction, [a] 2.
A chemist calls them second order rate laws because the rate is proportional to the product of two concentrations. If you plug this value into your equation, you find that d x d t = 0 which is also correct. Integrated rate law derivation” here (opens in new window). The above equation is known as integrated rate equation for zero order reactions.
Let's arbitrarily assume that [ a] ≥ [ b].
Here, the rate of reaction is directly proportional to [r]. In this type of reaction, the sum of the powers of concentrations of reactants in rate law is equal to 1, that is the rate of the reaction is proportional to the first power of the concentration of the reactant.