The integration of that second order differential rate law gives the second order integrated rate law. The integral form of the equation was obtained from the differential form and the full integration can be found here. This results in a reaction being 2nd order overall.
Rate constants were measured for the second order reaction
This is highly limited as more 2nd order reactions are the result of bimolecular steps occurring in a reaction.
−d[r] /dt = k[r] 2;
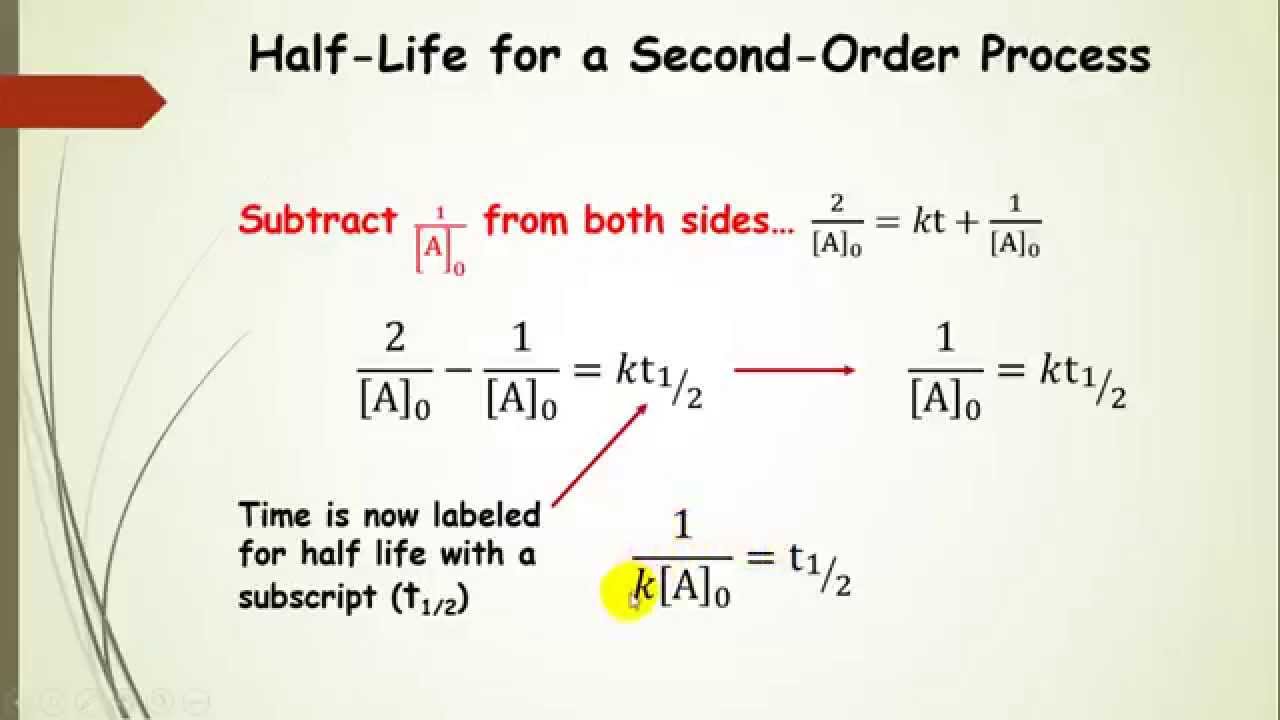
The integrated rate law for a first order reaction (sn 1) would be as follows: The second order integrated rate law is {eq}1/[a]_t = kt + 1/[a]_0 {/eq}. Zeroth order integrated rate law 2nd order reactions. 2nd order reaction integrated rate law 1 [𝐴𝐴] = 𝑘𝑘 +𝑑𝑑1 [𝐴𝐴]0 at time t = t1/2 [𝐴𝐴] = 1 2 [𝐴𝐴]0 therefore 1 [𝐴𝐴] = 2 ∙1 [𝐴𝐴]0 substitute for [a] 2 ∙1 [𝐴𝐴0] = 𝑘𝑘𝑑𝑑1⁄2+ 1 [𝐴𝐴]0 rearrange the terms 2 ∙1 [𝐴𝐴0] − 1 [𝐴𝐴0] = 𝑘𝑘𝑑𝑑1⁄2 1 [𝐴𝐴0]
[a] versus t (linear for a zero order reaction) ln [a] versus t (linear for a 1 st order.
Considering the scenario where one second order reactant forms a given product in a chemical reaction, the differential rate law equation can be written as follows: The rate constant for the. When a reaction is of second order with regard to a specific reactant, an increase in its quantity causes the rate to grow. [latex]\frac{1}{\left[a\right]}=kt+\frac{1}{{\left[a\right]}_{0}}[/latex] where the terms in the equation have their usual meanings as defined above.
In order to obtain the integrated rate equation, this differential form must be rearranged as follows:
This typically involves a collision between two different molecules. A much more limited case, is that of second order reactions. Where k is the rate constant plus the natural. \(\frac{1}{{[{\rm{r}}]}} = \,{\rm{kt}}\,{\rm{ + }}\,\frac{1}{{{{[{\rm{r}}]}_0}}}\) comparing the above equation with a straight line, \({\rm{y}}\, = \,{\rm{mx}}\,{\rm{ + c}}\) , a plot of the inverse of \({\rm{[r]}}\) as a function of time yields a straight line.
[ a ] 0 = 0.200 mol/l, k = 5.76 × × 10 −2 l/mol/min, and t = 10.0 min.
Jay courses 455 view detail preview site [] 2 0 1 x = 1 t k 4 note: Rate laws from graphs of concentration versus time (integrated rate laws) in order to determine the rate law for a reaction from a set of data consisting of concentration (or the values of some function of concentration) versus time, make three graphs. 2a products or a + b products (when [a] = [b]) , rate = k[a] 2 the integrated rate law is 1/[a] = kt + 1/[a o ]
− d [ r] d t = k [ r] 2.
\[\dfrac{1}{[a]}=kt+\dfrac{1}{[a]_0} \label{int2nd}\] where the terms in the equation have their usual meanings as defined earlier.