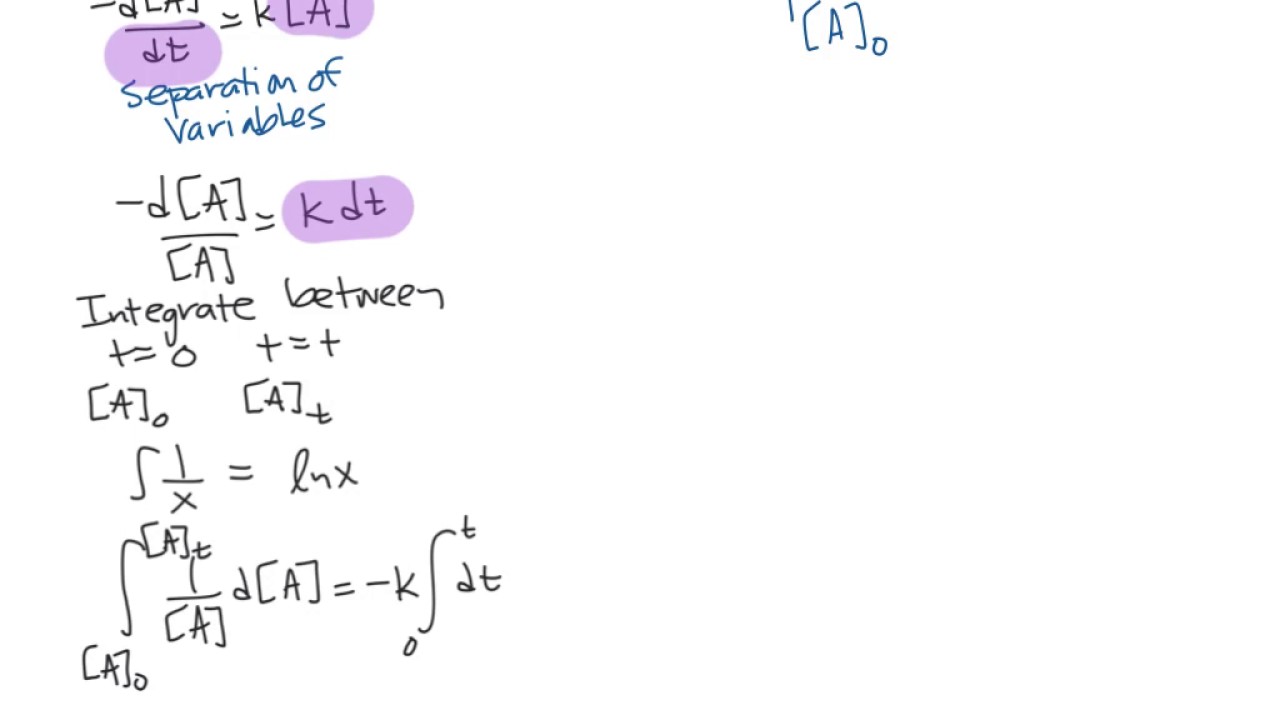Apparently the integrated form of d [ a] [ a] = ln. Rate = − d t d [r] = k [r] 1 rearrange above equation. Concentration at any moment of time can be given as, [a] = [ a] 0 e − k t.
integrated rate equation of first order reaction for
Now for the bit i need help with, the integration:
D [ a] [ a] = − k d t.
The common integrated rate laws. Integrate the above equation (i) between the limits of time t = 0 and time equal to t, while the concentration varies from initial concentration [a0] to [a] at the later time. T is the time elapsed since the reaction began; D [ a] d t = − k [ a] collect terms:
The first order rate integral[1] equation calculates the rate at which the reactants turn in to products.
[r] d [r] = − k × d t integrating on both sides of the given equation ∫ [r] d [r] = − k ∫ d t ln[r] = − k t + i. The integrated rate equation for a first order reaction is. [] = [] [] = ′ [] and [] = [] [], where ′ is the pseudo first order constant. Given the simple first order reaction a p derive the integrated rate law.
For a zero order reaction:
(1) where, [a] is the concentration of reactant at time t. C = loge [a] 0. (2) let [a] 0 be the initial concentration of the reactant a at time t = 0. Rate law can be expressed as, rate = k [a]1.
2a products or a + b products (when [a] = [b]) , rate = k[a] 2 the integrated rate law is 1/[a] = kt + 1/[a o] top.
(1) where i is integration constant at t = 0 the concentration of reactant [r] = [r] 0 where [r] 0 is initial concentration of reactant substituting in equation (1) we get A full integration of the equation can be found here. The integrated rate equation for the main product [c] is [] = [] [′ [] (′)], which is equivalent to [] [] [] = [] ′. [a] = [a] 0, at t = 0.
Where, k is the first order rate constant.
Thus, we can determine the concentration and rate of reaction at any moment with the help of integrated rate equation for zero and first order reaction. Because this equation has the form y = mx + b, a plot of the natural log of [a] as a function of time yields a straight line. First order reaction is a → product. 1 [a] = kt + 1 [a]0 y = mx + b.
The natural logarithm (in) of the concentration plotted against time gives a linear graph with a slope equal to the negative of the rate constant.
The equation (2) is integrated between limits [a] = [a] 0. Integration of this ordinary differential equation is elementary, giving: