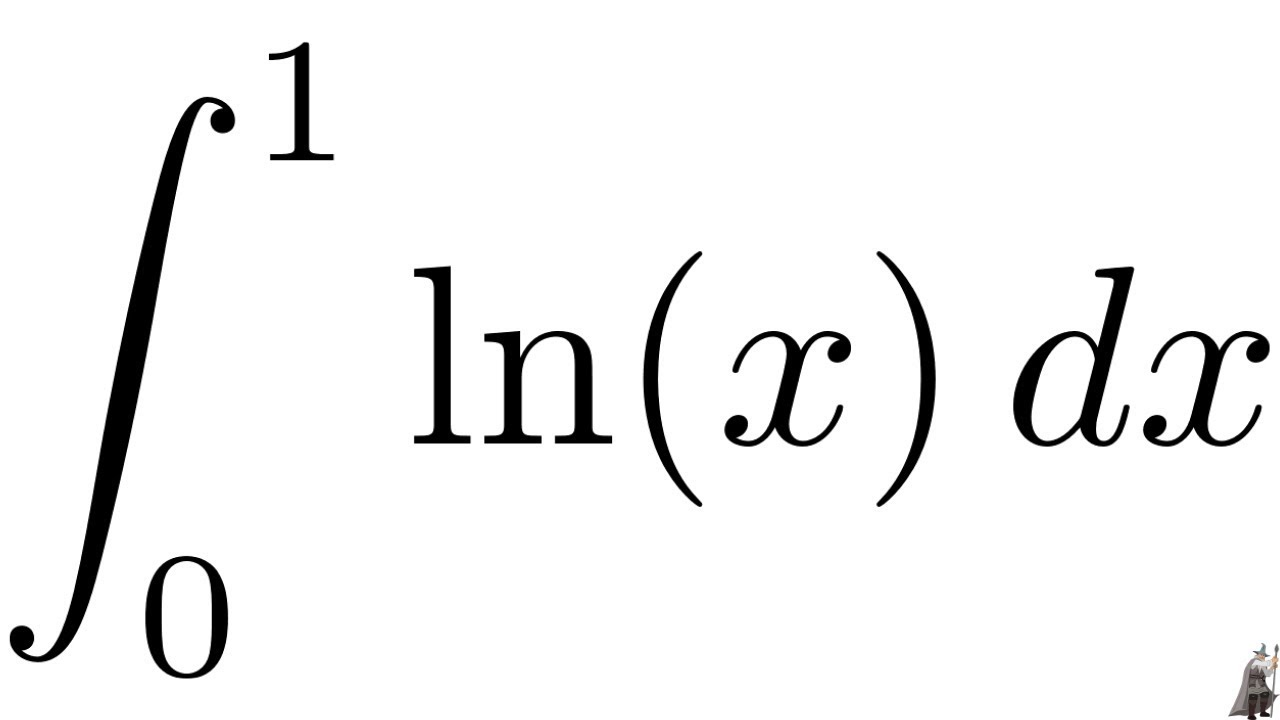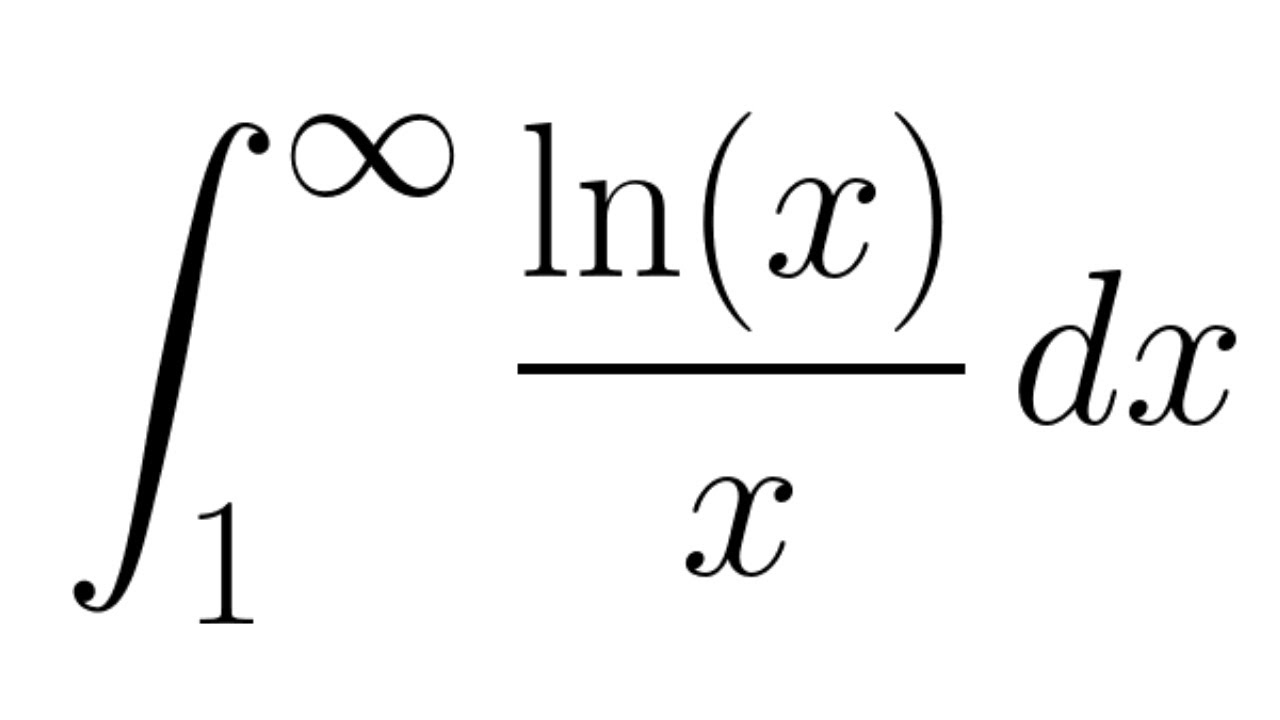I need to evaluate this integral using calculus of residues: Solved evaluate the integral from 1 to infinity of (ln | chegg.com. Determine if the integral integral_0^infinity cos^2(x) dx converges and compute its value.
Integral of ln(x+1) (substitution + by parts) YouTube
I get infinity and divergence.
Calculus introduction to integration definite and indefinite integrals.
Improper integral of lnx/x from 1 to infinityif you enjoyed this video please consider liking, sharing, and subscribing.you can also help support my channel. Show that integral_1^infinity 1/x ln x dx diverges. Learn how to solve definite integrals problems step by step online. I guess the cleanest way to get to the answer is to leave the series in terms of n and integrate that.
We can use integration by parts ∫udv = uv − ∫vdu.
I think i have to create a series and integrate term by term. The answer is supposed to be 0. Oct 29, 2016 the integral is not convergent. Type in any integral to get the solution, steps and graph
$$ \int_1^\infty \frac{\ln x} x \, dx $$ the integral is from $1$ to infinity.
$$\int_0^\infty\frac{\ln(x)}{1+x^4}\mathrm{d}x$$ i know i need to consider $\displaystyle \int_0^\infty$$\frac{\ln(z)}{1+z^4}\mathrm{. Use the substitution u = 1/x to show that integral_0^{infinity} {ln x} / {1 + x^2} dx = 0. Use the properties of logarithms to approximate the indicated logarithms, given that ln 2 ≈ 0.6931 and ln 3 ≈ 1.0986. Not sure how to set up from here.
This website uses cookies to ensure you get the best experience.
How do you integrate #ln(x)/(x)dx# from 1 to infinity? Let u = lnx and v = x5 5. I started with the substitution. I'm pretty sure that cut is the result of using the principal branch of $\log(1+z^{2})$.
Determine for what value that integral_1^infinity dx/xp converges and what value it converges to.
Type in any integral to get the solution, free steps and graph Continue reading the integral of ln(x+1)/(x^2+1). Show that integral_1^infinity 1/x ln x(x)^2 dx converges and compute its value. Solve by taking the limit as $t$ approaches infinity.
= x5 5 × lnx −∫ x5 5 × dx x.
For teachers for schools for working scholars® for. Either way i am stuck here. $\begingroup$ @ron you directed me to your post, so i hope you're willing to answer some of my questions. First, we must identify a section within the integral with a new variable (let's call it u), which when substituted makes the integral easier.
= lnx ×x5 5 − 1 5∫x4dx.
2 answers steve m oct 29, 2016 you can't as the integral is divergent. By signing up, you'll get thousands of. Evaluate the integral from 1 to infinity of. I don't think the branch of $\log(1+z^{2})$ you used coincides with that cut.
Complex contour integral of ln(x)/(x^2+1)^2 from 0 to infinity more complex analysis:
Integrate (ln(x)/x from 1 to \infty. ∫lnx × x4dx = ∫udv = uv −∫vdu.