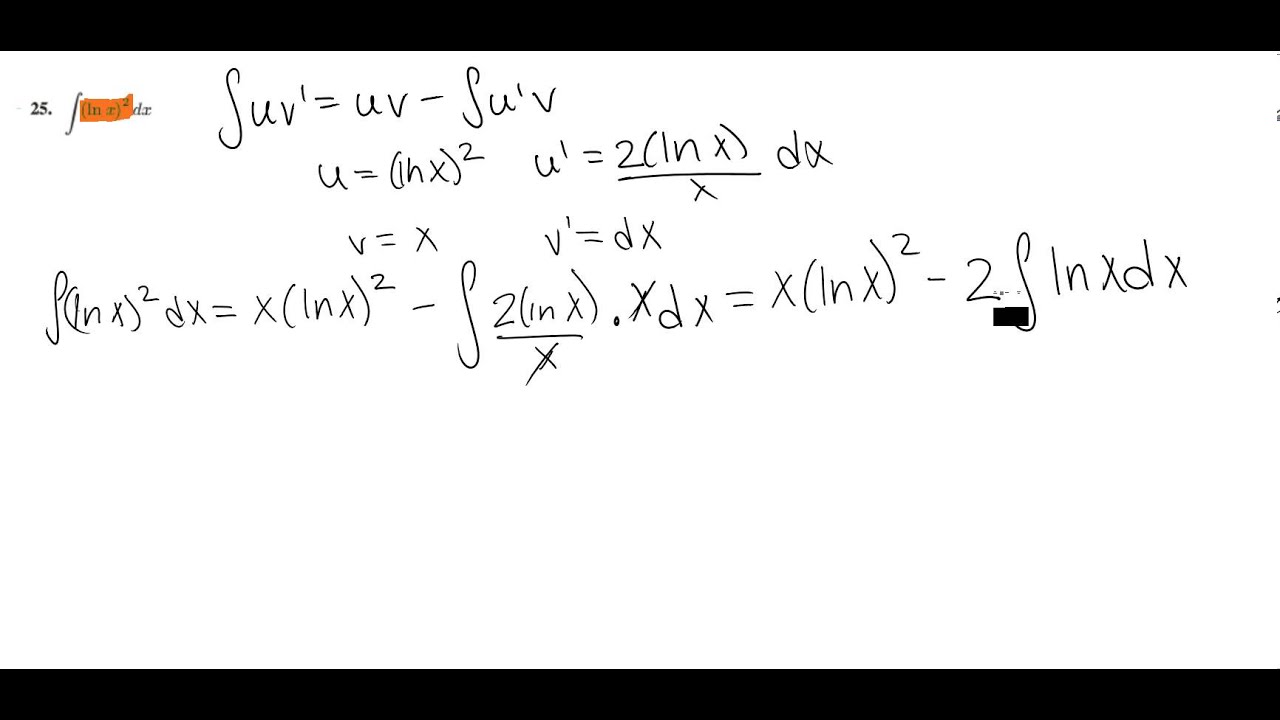How do you integrate #int ln^(6)x/x dx#? If you mean (1+2x)/ (x+x^2), you are correct. We review their content and use your feedback to keep the quality high.
How to integrate ln x (Integration by Parts) YouTube
U = ln x, dv =.
Integral of ln(3x)dx (integration by parts).
Here the first function is ln. To find the integral of (ln x) 2, we will use the integration by. Evaluate the integral using integration by parts with the indicated choices of u and dv. The indefinite integral of ln(x) is given as:
To evaluate the given integral, let u= lnx u = ln.
Integral square root x ln x dx; I = ∫ x ln. Substitute the above expressions to the given integral and simplify. Differentiating both sides, we have:
Integration of x ln x.
There is no integral rule or shortcut that directly gets us to the integral of ln(x). Integrate the original integrand by parts: Find the indefinite integral integral (ln (x))^5/2/x dx + c find the indefinite integral. Now multiply that by x (to get vdu) and see if you can integrate that (it's a bit tricky).
Ahhh, your notation had me confused for a second.
X and the second function is x. Click here👆to get an answer to your question ️ solve : Int x^x ln (ex) dx | maths quest. Join / login >> class 12 >> maths >> integrals >> integration by parts >> solve :
Integral of sin( ln( x)) d x.
Experts are tested by chegg as specialists in their subject area. Your first 5 questions are on us! Integration the following table of integrals can be used without any further justi cation. #u = lnx# #du = 1/xdx#.
Z ax dx = 1 ln(a) ax +c ) z cos(x)dx = sin(x) +c z sec2(x)dx = tan(x) +c z sec(x)tan(x)dx = sec(x)+c z sin(x)dx = −cos(x)+c
Integral of ln (x+1) \square! List of basic integrals z kdx = kx+c z xn dx = 1 n+ 1 xn+1 +c (n 6= −1) z 1 x dx = ln|x|+c z ex dx = ex +c (and more generally: Modified 6 years, 9 months ago. Z xn dx = 1 n+ 1 xn+1 + c (n 6= 1) z 1 x dx = lnjxj+ c z 1 ax+ b dx = 1 a lnjax+ bj+ c z ex dx = ex + c z
Int x^x ln (ex) dx.
But the expression inside the ln is x^2+x and not x. Jun 8, 2015 first, notice that you can rewrite this as: Your first 5 questions are on us! Calculus techniques of integration integration by substitution.
If taking the definite integral of ln(x), you don’t need the c.
Integral of ln (x) \square! Du = 1 x dx d u = 1 x d x. The integral of x ln x is of the form. Integration by parts is much easier to do in terms of functions and derivatives rather than differentials, yet the above answerer has chosen the more complicated way.
So you have to apply the general rule for differentiating ln (f (x)).
Let f' (x) = 1. Find the formula of integral of ln x whole square using the formula of integral of ln x.
