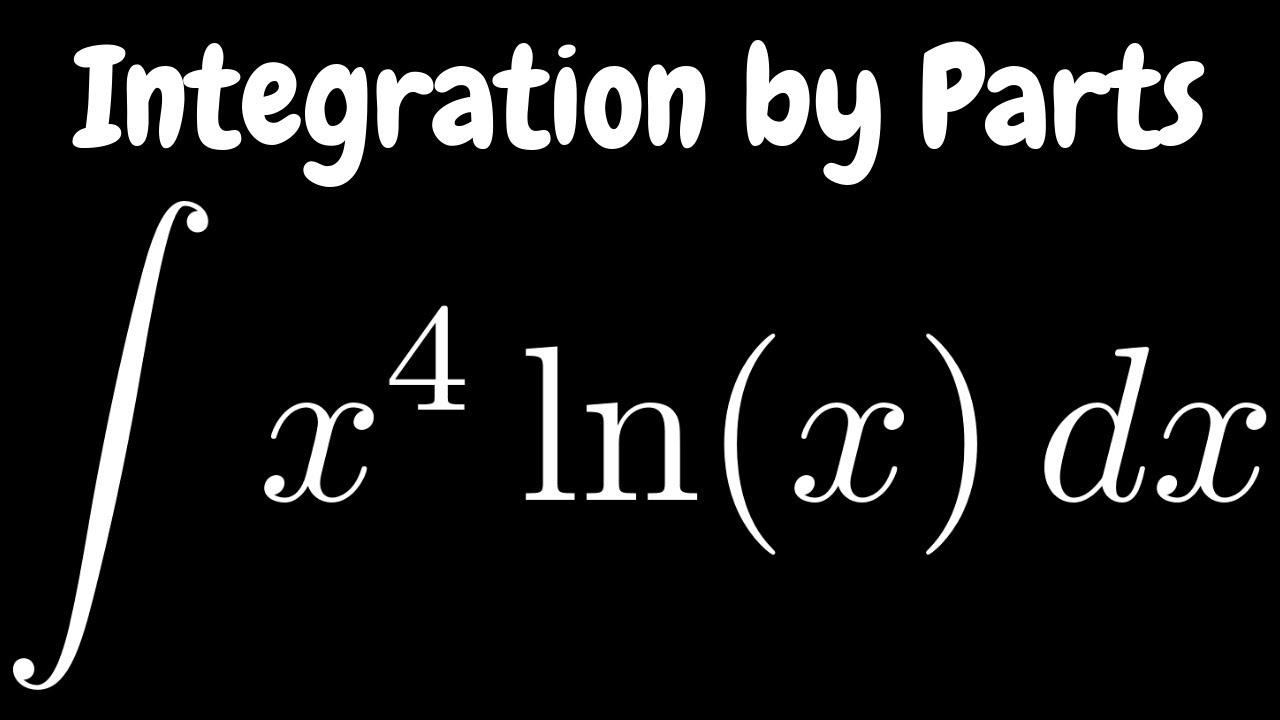Integrate Ln Xx By Parts Integration Of (lnx)^2 (Student) YouTube

You will see plenty of examples soon, but first let us see the rule: For u i am choosing ln x, and therefore its derivative du/dx is 1/x. Now i can't figure out how to integrate ∫ (x (2x+14))/x^2+14x+24.

Integration of (ln x)^2 Integration by parts YouTube

X ( ∫ x d x)] d x ⇒ i = ln.

Apply integration by parts formula, we have.

U = ln (x), dv = dx. Using the above formula, equation (i) becomes. The derivative of ln(x) is (1/x) dx, and the antiderivative of x 2 is (⅓)x 3. ( x) d x, it is probably easiest to compute the antiderivative ∫ x ln.

You haven't technically used integration by parts, all you've used is the fundamental theorem of calculus and the product rule (but that's all ibp is anyway, just more generally).

I thought i might have to use integration by parts again but it's not working out. Now that we have all the variables, let’s plug them into the integration by parts equation: D/dx [f (x)·g (x)] = f' (x)·g (x) + f (x)·g' (x) becomes. ∫ (lnx)( 1 x2) dx = (lnx)( − 1 x) −∫ ( − 1 x)( 1 x) dx.

In order to compute the definite integral ∫ 1 e x ln.

Ln (x) dx = u dv. To do this integral we will need to use integration by parts so let’s derive the integration by parts formula. Using the formula above, equation (i) becomes. \int x\cos\left (x\right)dx ∫ xcos(x)dx by applying integration by parts method to calculate the integral of the product of two functions, using the following formula.

Previously, we found ∫ x ln.

Integration by parts with a definite integral. Evaluate the integral using integration by parts with the indicated choices of u and dv. Same deal with this short form notation for integration by parts. Any help would be greatly appreciated.

(fg)' = f'g + fg'.

Integration by parts xln x. Let {u = lnx ⇒ du dx = 1 x dv dx = 1 x2 ⇒ v = − 1 x. ∫ x 5 ln in x dx =‍ ∫ ln in x x 5 dx. ∫ 6x √(x−3) dx 2.) use integration by parts to evaluate the integral:

∫ (f g)′dx =∫ f ′g +f g′dx ∫ ( f g) ′ d x = ∫ f ′ g + f g ′ d x.

∫3s^2 e^−2s ds 3.) use integration by parts to evaluate the integral: ∫ u v dx = u ∫ v dx − ∫ u' ( ∫ v dx) dx. Then once i substitute, i get: This is a standard proof that you can look up in the formula sheet if you cannot remember it.

∫ (u)( dv dx) dx = (u)(v) − ∫ (v)( du dx) dx.

U = ln x, dv =. ∫x3 ln x dx *since lnx is a logarithmic function and x3 is an algebraic function, let: Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways. I = ∫ lnx x2 dx.

And use integration by parts.

However, we generally use integration by parts instead of the substitution method for every function. ( x) d x = x ln. Yes, we can use integration by parts for any integral in the process of integrating any function. And some functions can only be integrated using integration by parts, for example, logarithm function (i.e., ln(x)).

Using the formula for integration by parts, we have.

∴ i = − lnx x +∫ 1 x2 dx. Substitute u=ln (x), v=x, and du= (1/x)dx. We’ll start with the product rule. By using this website, you agree to our cookie policy.

X − 1 4 x 2 + c.

Ln (x) dx = u dv. This is ideal if you are just starting out. And use integration by parts. Then plugging into the ibp formula:

This one a bit deeper:

U = lnx (l comes before a in liate) dv = x3 dx du = x 1 dx v = ∫ = 4 4 x3dx x ∫∫x3 ln xdx = uv− vdu dx x x x x 1 4 4 (ln ) 4 4 = − ∫ x dx x = x − ∫ 3 4 4 1 4 (ln ) c x x x = − + 4 4 1 (ln ). Use integration by parts to evaluate the integral: Du = (1/x) dx, v = x. I've tried multiplying out, factoring.

We can then apply integration by parts:

We can solve the integral. ∫3s^2 e^−2s ds 3.) use. Du = (1/x) dx, v = x. All that’s left now is to simplify!

Now, integrate both sides of this.

Using integration by parts to find the integral of ln x ∫ x cos ⁡ ( x) d x. This article talks about the development of integration by parts: ∫ u ⋅ d v = u ⋅ v − ∫ v ⋅ d u.

∫x 2 ln(x)dx=ln(x)⋅(⅓)x 3 −∫(⅓)x 3 ⋅(1/x) dx.

Integral square root x ln x dx; We can also sometimes use integration by parts when we want to integrate a function that cannot be split into the product of two things. Let f (x)=lnx and g' (x)= x 5 , then f' (x)= 1 x and g (x)= x 6 6. Substitute u=ln (x), v=x, and du= (1/x)dx.