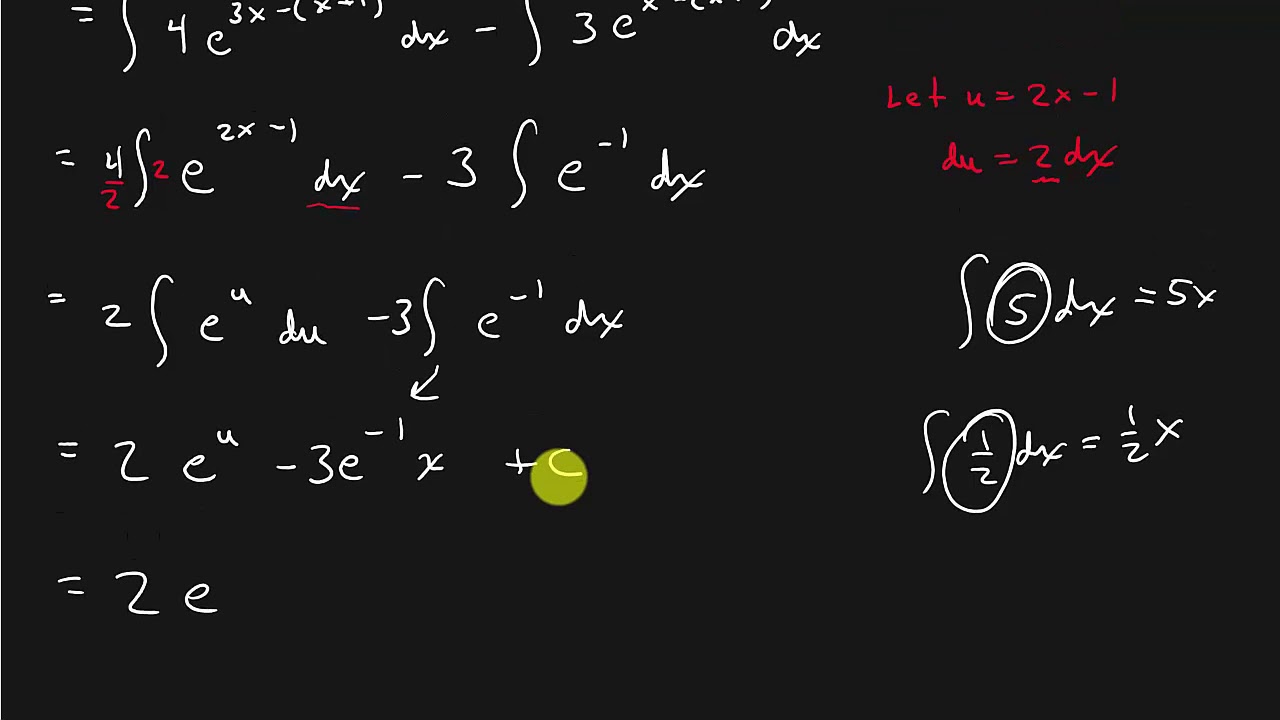Table of integrals basic forms (1)!xndx= 1 n+1 xn+1 (2) 1 x!dx=lnx (3)!udv=uv!vdu (4) u(x)v!(x)dx=u(x)v(x)#v(x)u!(x)dx rational functions (5) 1 ax+b!dx= 1 a ln(ax+b) (6) 1 (x+a)2!dx= 1 x+a (7)!(x+a)ndx=(x+a)n a 1+n + x 1+n #$ % &', n!1 (8)!x(x+a)ndx= (x+a)1+n(nx+xa) (n+2)(n+1) (9) dx!1+x2 =tan1x (10) dx!a2+x2 = 1 a tan1(x/a) (11) xdx!a2+x2. These formulas lead immediately to the following indefinite integrals : Solved exercises of integrals of exponential functions.
Indefinite Integrals ∫ 2^(3 log_2x ) dx Exponential
Table of integrals 0 (1)suedusu (s + 1) = s (s) (n + 1) = n!
Table of available exponential integrals.
Integrals of exponential functions calculator online with solution and steps. Detailed step by step solutions to your integrals of exponential functions problems online with our math solver and calculator. ∫ exdx = ex+c ∫ axdx = ax lna +c ∫ e x d x = e x + c ∫ a x d x = a x ln a + c. Calculates a table of the exponential integral ei(x) and draws the chart.
A third recursion formula, intermediate in character between (3) and (5), was given by gram £3].
Equations (5) and (7) were employed to compute the values of e~xei(x) The fundamental theorem of calculus establishes the relationship between indefinite and definite. The number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the derivative. Integrals with exponentials z eaxdx = 1 a eax (50) z p xeaxdx = 1 a p xeax + i p ⇡ 2a3/2 erf i p ax, where erf(x)= 2 p ⇡ z x 0 et 2 dt (51) xe xdx =(x 1)e (52) z xeaxdx = x a 1 a2 eax (53) z x2exdx =.
The following integrals, in which a and b are real, can be evaluated in terms of the real and imaginary components of the exponential integral :
= 1 2 2 for even 0 for odd ue dunu gn n n some specialized results appear in the extended integral table below. Table of the exponential integral el (x) 11 together with the value ro(h) = 1 — e~h. E−ax2dx= 1 2 π a # $% & ’(1 2 0 ∞ ∫ ax xe−2dx= 1 2a 0 ∞ ∫ x2e−ax2dx= 1 4a π a # $% & ’(1 2 0 ∞ ∫ x3e−ax2dx= 1 2a2 0 ∞ ∫ x2ne−ax2dx= 1⋅3⋅5⋅⋅⋅(2n−1) 2n+1an π a $ %& ’ 1 2 0 ∞ ∫ x2n+1e−ax2dx= n! Can be used, for example, the exponential integral eihzl can be defined by the following formula (see the following sections for the corresponding series for the other integrals):
Where possible the integrals are expressed in closed form.
Table of integrals∗ basic forms z xndx = 1 n+ 1 xn+1 (1) z 1 x dx= lnjxj (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2 dx= ln(1 x+ a (5) z (x+. Find the integral r 23x+1 dx: The following problems involve the integration of exponential functions. A substantial portion of the results are new.
Also included are several integrals which are expressed in series expansions.
A table of integrals of the exponential integral. A quick look at the exponential integrals here is a quick look at the graphics for the exponential integrals along the real axis. , where a is any positive constant not equal to 1 and is the natural (base e) logarithm of a. Although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total growth.
The following table is a collection of some frequently occurring integrals in quantum mechanics among other applications involving powers, exponentials, logarithms and exponential integrals.
A table of integrals involving powers, exponentials, logarithms, and the exponential integral table integrals involving powers, exponentials, logarithms and the exponential integral. (jet propulsion lab., california inst. The nature of the antiderivative of ex e x makes it fairly easy to identify what to choose as u u. 2 1 2 0 1 ( ) ( )2 gn u e dunu n 1 ()2 (1) = 0!
Integral of ex:obtain 1 2 z e udu= 1 2 e + c= 1 2 ex2+1 + c:
Integral and derivative table in this table, a is a constant, while u, v, w are functions. The derivatives are expressed as derivatives with respect to an arbitrary variable x. Use the substitution u= 3x+ 1 )du= 3dx)du 3 = dx:the integral becomes r 2udu 3 = 1 3 r 2u du:the integrand 2u is now simple and you can integrate it using the formula for integral of ax with a= 2:obtain 1 3 z 2udu= 1 3 1 ln2 2u+ c= 1 3ln2 23x+1 + c: Table of useful integrals, etc.
Exponential integral are also available [6].
Exponential functions can be integrated using the following formulas. If only one e e exists, choose the exponent of e e as u u.