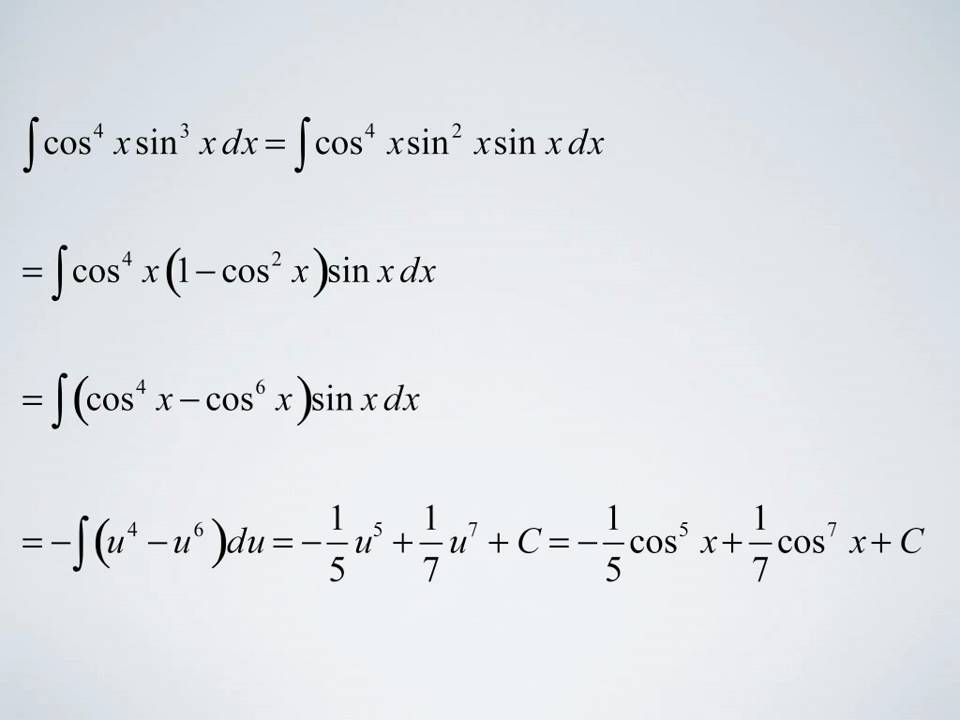X by the substitution of du, d u, and be left with an even number of cosine powers. Differentiability and the chain rule differentiability the first case of the chain rule chain rule, general case video: 1 + cot 2 x = csc 2 x.
2.1.11.12.4 Chapter 4 Indefinite Integrals
Use either 1 1 or 2 2 (both will work).
Integrals involving sec(x) and tan(x):
A.) b.) c.) so that ; Z sin(2x)cos(5x) dx here, we use the sum formulas: Ln | sin x | + c: Recall the definitions of the trigonometric functions.
Integrals involving sin(x) and cos(x):
Sets found in the same folder. ∫ cot n x d x = ∫ cot n − 2 x cot 2 x d x = ∫ cot n − 2 x ( csc 2 x − 1) d x = − cot n − 1 x n − 1 − ∫ cot n − 2 x d x. ∫ (f + g) dx: Trigonometric integrals r sin(x)dx = cos(x)+c r csc(x)dx =ln|csc(x)cot(x)|+c r cos(x)dx =sin(x)+c r sec(x)dx =ln|sec(x)+tan(x)|+c r tan(x)dx =ln|sec(x)|+c r cot(x)dx =ln|sin(x)|+c power reduction formulas inverse trig integrals r sinn(x)=1 n sin n1(x)cos(x)+n 1 n r sinn2(x)dx r sin1(x)dx = xsin1(x)+ p 1x2 +c r cosn(x)=1 n cos n 1(x)sin(x)+n 1 n r cosn 2(x)dx.
This doesn’t always work, but it’s a good place to start.
Now recall the trig identity, cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 − cos 2 x. Let’s first notice that we could write the integral as follows, ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x ∫ sin 5 x d x = ∫ sin 4 x sin x d x = ∫ ( sin 2 x) 2 sin x d x. Integrals of the form ∫ cot n x d x. Both m m and n n are even:
With de nite integrals, the formula becomes z b a udv= u(x)v(x)]b a z b a vdu:
X /2 + sin (2 x)/4 + c = (x + sin x ∙ cos x)/2 + c: Generally, if the function is any trigonometric function, and is its derivative, ∫ a cos n x d x = a n sin n x + c {\displaystyle \int a\cos nx\,dx={\frac {a}{n}}\sin nx+c} in all formulas the constant a is assumed to be nonzero, and c denotes the constant of integration. Sal simply rewrote 11π/2 as 3π/2 + 4π. Depending upon your instructor, you may be expected to memorize these antiderivatives.
Contents 1 integrals involving only sine 2 integrands involving only.
X ( = 1 − u 2) to replace the leftover cosines. Sin( )cos( ) = 1 2 (sin( + ) + sin( )) doing a similar thing to the cos formula, one gets rules that will help for integrals of the form cos( )cos( ) and sin( )sin( ). Generally, if the function is any trigonometric function, and is its derivative, in all formulas the constant a is assumed to be nonzero, and c denotes the constant of integration. Convert the remaining factors to cos( )x (using sin 1 cos22x x.) 1.
Here are some hints to help you remember the trig differentiation and integration rules:
X n+1 n+1 + c: For a complete list of antiderivative functions, see lists of integrals. Some of the following trigonometry identities may be needed. E.) f.) so that ;
X d x = sin.
Just like f (0) = f (2π), we can also say that f (3π/2) =. Power rule (n≠−1) ∫ x n dx: Adding the two, one gets: If the integral contains the following root use the given substitution and formula to convert into an integral involving trig functions.
Sometimes, use of a trigonometric substitution enables an integral to be found.
∫sec x dx = ln|tan x + sec x| + c. ∫cos x dx = sin x + c. If the power of the sine is odd and positive: The power of the integrand can be reduced using the trigonometric identity.
Integrals of trig functions antiderivatives of basic trigonometric functions product of sines and cosines (mixed even and odd powers or only odd powers).
X = 1 − sin 2. ∫ du u√u2−a2 = 1 a sec−1 u a +c ∫ d u u u 2 − a 2 = 1 a sec − 1 u a + c. Use cos2x = 1 2(1+cos(2x)) cos 2. (this just means we nd the antiderivative using ibp and then plug in the limits of integration the way we do with other de nite integrals.
When the trig functions start with “ c ”, the differentiation or integration is negative (cos and csc).
Save a du x dx sin( ) ii. Integrals requiring the use of trigonometric identities the trigonometric identities we shall use in this section, or which are required to complete the exercises, are summarised here: This makes f (0) = f (2π) = f (4π) and etc. Ln | sec x + tan x | + c:
In the video, we work out the antiderivatives of the four remaining trig functions.
Both m m and n n are odd: Derivative rules involving inverse trigonometric functions. 16 x2 49 x2 dx ∫ − 22 x = ⇒ =33sinθ dx dcosθθ Use cos2x = 1−sin2x (= 1−u2) cos 2.
It is a ton easier to know the cosine of a more familiar value, namely those that are 0<x<2π.
∫tan x dx = ln|sec x| + c. Exponential and then whatever is left is dv. The following integration formulas yield inverse trigonometric functions: ∫ du a2+u2 = 1 a tan−1 u a +c ∫ d u a 2 + u 2 = 1 a tan − 1 u a + c.
This means that every 2π, the function repeats.
Below are the list of few formulas for the integration of trigonometric functions: 2 22 a sin b a bx x− ⇒= θ cos 1 sin22θθ= − 22 2 a sec b bx a x− ⇒= θ tan sec 122θθ= − 2 22 a tan b a bx x+ ⇒= θ sec 1 tan2 2θθ= + ex. The antiderivatives of tangent and cotangent are easy to compute, but not so much secant and cosecant. For the functions other than sin and cos , there’s always either one tan and two secants , or one cot and two cosecants on either side of the formula.
∫cot x dx = ln|sin x|.
∫ du √a2−u2 = sin−1 u a +c ∫ d u a 2 − u 2 = sin − 1 u a + c.