Find d u d x d u d x. Integration of the secant tangent function is an important integral formula in integral calculus, and this integral belongs to the trigonometric formulae. >> integrals >> integration by substitution >> evaluate inttanx/(secx + tanx) dx.
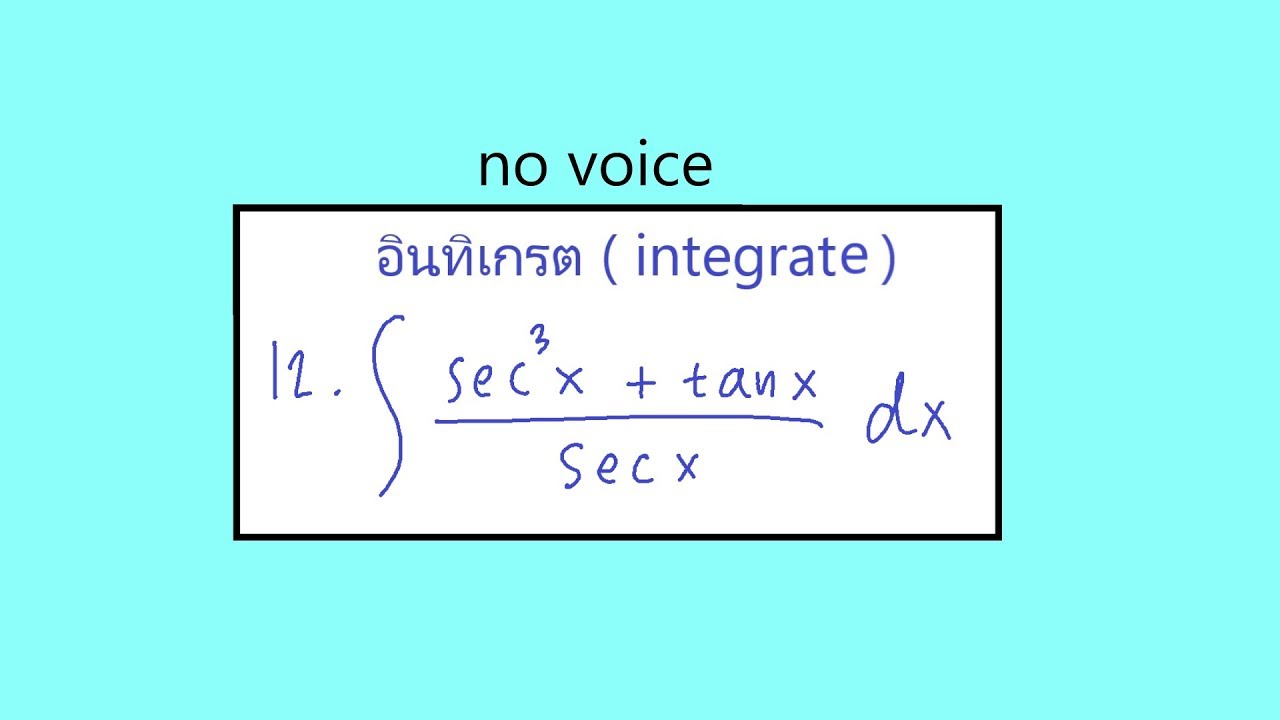
integrate 12 ((secx)^2))+ tanx)/(secx))dx YouTube
X) 11 / 2 { 1 11 + 1 7 ( sec.
Evaluate the integral of sec x tan x + sec 2 x.
X d x = sec. We know that the integration of sec x tan x is sec x + c and the integral of sec 2 x is tan x + c. ∫(sec x tan x + sec 2 x) dx = ∫sec x tan x dx + ∫sec 2 x dx = sec x + tan x + c Integral of tan^2 (x) \square!
I = ∫ sec2xdx (secx+tanx)9 2 ⇒ let secx+tanx = z (secxtanx+sec2x)dx = dz secx(secx+tanx)dx =dz secxdx = dz z also.
Tan (x) draw graph edit expression direct link to this page. The integration of secant tangent is of the form. This just cancels in the end to 0 = 0. The first one is simple, but what is the integral of.
= ln ∣ sec x − tan x ∣ 1 + ln ∣ sec x ∣ + c [sec 2 x − tan 2 x = 1 ⇒ (s e c x + t a n x) = s e c x − t a n x 1 ] = − ln ∣ sec x − tan x ∣ + ln ∣ sec x ∣ + c was this answer helpful?
Sometimes an approximation to a definite integral is. Specifically, multiply both numerator and denominator by cos (x) to get sin^2 (x)cos (x)/cos^4 (x). \[\int \tan^{2}x\sec{x} \, dx\] +. The derivative of sec ( x) sec ( x) with respect to x x is sec ( x) tan ( x) sec ( x) tan ( x).
According to integral calculus, it can be expressed in mathematical form as follows.
Replace all occurrences of u u with sec(x) sec ( x). The derivative of sec ( x) sec ( x) with respect to x x is sec ( x) tan ( x) sec ( x) tan ( x). The definite integral of from to , denoted , is defined to be the signed area between and the axis, from to. Rewrite the problem using u u and d u d u.
Let us assume that log.
Geometrical interpretation of indefinite integral. Students (upto class 10+2) preparing for all government exams, cbse board exam, icse board exam, state board exam, jee (mains+advance) and neet can ask questions from any subject and get quick answers by. Differentiate sec ( x) sec ( x). D/dx (int f (x) dx) = f (x) the integral of the product of a constant and a function = the constant x integral of function.
By the power rule, the integral of u3 u 3 with respect to u u is 1 4u4.
Your first 5 questions are on us! Sec x = sec x * [ (sec x + tan x) / (sec x + tan x)] = g(x) ln (sec x + tan x) = integral of g(x)dx so, let u = ln (sec x + tan x) du = sec x * [sec x + tan x] / [sec x + tan x] dx integrating u du = u^2/2 = [ln (sec x +. X) 2 } + c. It also allows to draw graphs of the function and its integral.
Multiply secx in bracket =int.
Also, the integral of a sum of two functions is equal to the sum of integrals of the two functions. Comparison between differentiation and integration. X 2 × 1 cos 2. The collection of all primitives of product of $\sec{x}$ and $\tan{x}$ function is called as the integration of product of secant and tan functions.
Evaluate ∫ (sec x + tan x) tan x d x.
Rewrite the problem using u u and d u d u. Int {f (x) pm g (x)} dx = int f (x) dx pm int g (x) dx. Tan (x)= sin (x)/cos (x) and sec (x)= 1/cos (x) so tan^2 (x) sec (x)= sin^2 (x)/cos^3 (x). A unique platform where students can interact with teachers/experts/students to get solutions to their queries.
Both types of integrals are tied together by the fundamental theorem of calculus.
Please feel free to post as many doubts on our discussion forum as you can. I've tried a few things, the first being integration by parts with u = ln (secx + tanx+) and dv = dx. In this method of integration by substitution, any given integral is transformed into a simple form of integral by substituting the independent variable by others. By the power rule, the integral of u4 u 4 with respect to u u is 1 5u5 1 5 u 5.
That involves cosine to an odd power so we can factor out one to use with a substitution.
Integral of sec (x)^2 by x: Differentiate sec ( x) sec ( x).