Ex 7.2, 34 integrate √ (tan𝑥 )/sin〖𝑥 cos𝑥 〗 simplifying the function √ (tan𝑥 )/sin〖𝑥 cos𝑥 〗 = √ (tan𝑥 )/ (sin〖𝑥 cos𝑥 〗. The first method i will describe is the mostelegant, but requires. Integrate sqrt (tan (x)) natural language.
`int sec x tan x sqrt(tan^(2) x4) dx` YouTube
Well hoot, what you have done is considered tan(x)=u and integrated u^1/2 du.but you haven't changed dx to du.you can do this as [tex]u=tan(x)^{\frac{1}{2}}[/tex] [tex]\frac{du}{dx}=\frac{sec^2(x)}{2\sqrt{tan(x)}}[/tex] and then find du and so the integrand changes.
X d x = ∫ 2 t 2 d t 1 + t 4 = ∫ 1 2 ( 1 1 − 2 t + t 2 + 1 1 + 2 t + t 2 − 1 2 ( 2 − 2 t 1 − 2 t + t 2 + 2 + 2 t 1 + 2 t + t 2)) d t = 1 2 arctan.
So, sec 2 x = d t d x. = 2 t 1 2 + c. { a s ∫ x n d x = x n + 1 n + 1 + c } = t 1 2 1 2 + c. See the image for solution thanks
This means ∫π 0 sin(x)dx= (−cos(π))−(−cos(0)) =2 ∫ 0 π sin.
( x) d x = ( − c o s ( π)) − ( − c o s ( 0)) = 2. Integral sqrt tan x sec^4 x dx; A common way to do so is to place thin rectangles under the curve and add the signed areas together. = ∫ ( t) − 1 2.
⇒ integral ∫ 2t 2 / (1 + t 4) dt.
⇒ dx = [2t / (1 + t 4 )]dt. Experts are tested by chegg as specialists in their subject area. X = t 2, ∫ tan. D t sec 2 x.
⇒ sec 2 x dx = 2t dt.
#int\ 1/sqrt(tanx)\ dx=int\ 1/sqrt(tanx)*(2sqrt(tanx))/sec^2x\ du=# Click here👆to get an answer to your question ️ int^ (√(tanx)+√(cotx))dx = There are two methods to deal with 𝑡𝑎𝑛𝑥 (1) convert into 𝑠𝑖𝑛𝑥 and 𝑐𝑜𝑠𝑥 ,. Integral of sqrt (x) \square!
Cos^2𝑥/cos𝑥 ) = √ (tan𝑥 )/ (cos^2𝑥.
X − 1) + 1 2 arctan. Sometimes an approximation to a definite integral is desired. Tanx=t^2, so that, sec^2xdx=2tdt, or, dx=(2tdt)/sec^2x=(2tdt)/(1+tan^2x)=(2tdt)/(1+t^4). Integral sqrt tan x sec^4 x dx.
We review their content and use your feedback to keep.
Use math input mode to directly enter textbook math notation. The square root of tan^2x is just tanx and that is much nicer. Up to 3% cash back integral of the square root of tan (x) from 0 to pi/2. ∴ ∫ ( tan x) − 1 2.
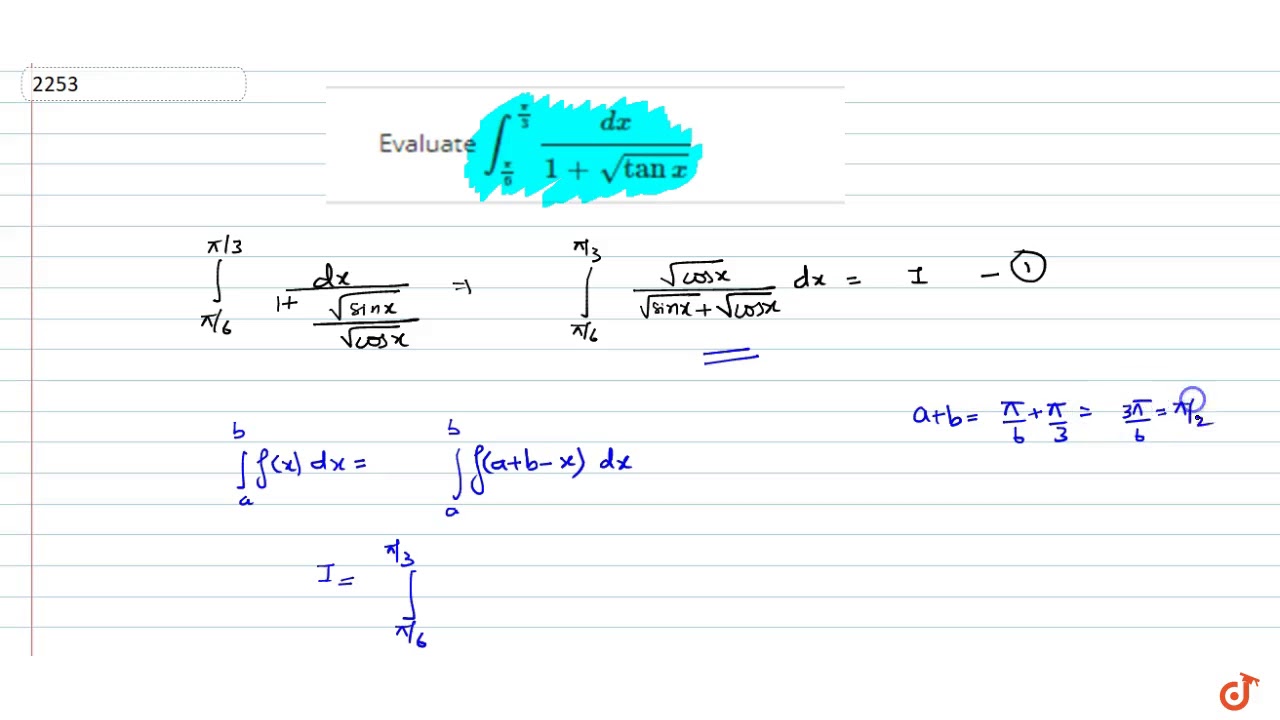
Statement i the value of the integral ∫(x → pi/3,pi/6)dx/(1 + √tanx) is equal to pi/6.
Let tan x = t. Let tan x = t 2. See the answer see the answer see the answer done loading. I'm taking requests, so please comment requests here or pm me directly.
This intimidating integration of square root of tanx can be solved by distinct techniques.
Just follow orion's thread to see how it is done. Substitute y = `sqrt(tan x)` => `((sqrt tan x)*(14*tan x + 6*tan^3 x))/21` the required integral is `((sqrt tan x)(14*tan x + 6*tan^3 x))/21 + c` Please 'like' if you enjoy and 'subscribe' if you would like to see more. ⇒ dx = d t sec 2 x.
∫ (tan x + cot x ) d x.
= ∫ ( t) − 1 2 dt. Cos𝑥/cos𝑥 ) = √ (tan𝑥 )/ (sin𝑥. #(du)/dx=(sec^2(x))/(2sqrt(tanx))# so we divide by that to integrate with respect to #u# (and remember, dividing by a fraction is the same as multiplying by its reciprocal): Show transcribed image text expert answer.
This problem has been solved!
Integrate wrt x sin 3 x cos 3 x. Integration of sqrt(tanx) + sqrt(cotx) | indefinite integration problem In this video, the definite integral of sqrt (tan (x)) from 0 to pi/2 is evaluated using the beta function, gamma function, and euler's reflection formula.