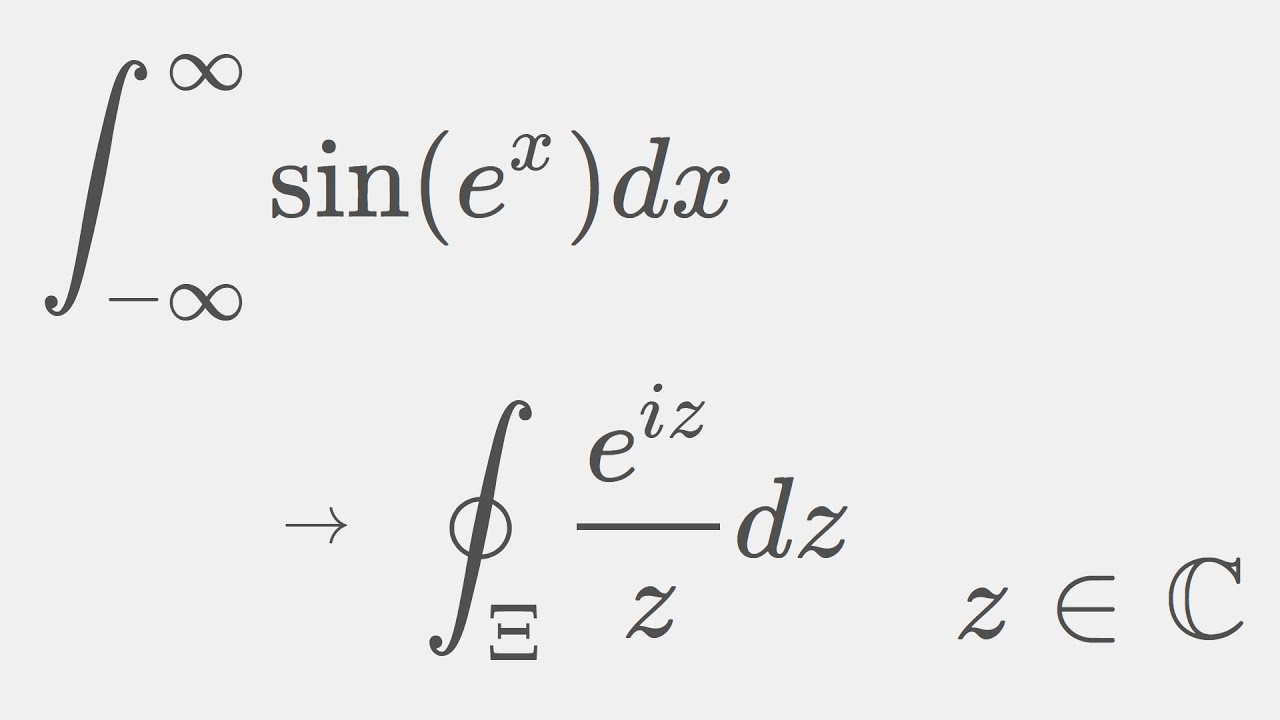Instead i’m using special functions li. Table of useful integrals, etc. And thus by the lemma.
Integral of sin(x^n) from 0 to infinity Part 1 of 3
This integral pops up everywhere, and it has an endearing number of derivations.
D^3/dx^3 1/sin(x) have a question about using wolfram|alpha?
E−ax2dx= 1 2 π a # $% & ’(1 2 0 ∞ ∫ ax xe−2dx= 1 2a 0 ∞ ∫ x2e−ax2dx= 1 4a π a # $% & ’(1 2 0 ∞ ∫ x3e−ax2dx= 1 2a2 0 ∞ ∫ x2ne−ax2dx= 1⋅3⋅5⋅⋅⋅(2n−1) 2n+1an π a $ %& ’ 1 2 0 ∞ ∫ x2n+1e−ax2dx= n! That is [tex]si(\infty) = \pi/2[/tex]. (1) ϕ(λ) = ∫ ∞ 0 sin(x)e−λx dx = 1 1+λ2. The integral of from 0 to infinity of cos(x)/sqrt(x), or sin(x)/sqrt(x) is well known to be sqrt(pi/2).
We will look at five of them before putting the formula (1) to work on other prob.
Integral from 0 to+infinity of sin (x)=1. Proof of various integral properties. Type in any integral to get the solution, steps and graph this website uses cookies to ensure you get the best experience. Contact pro premium expert support ».
Your first 5 questions are on us!
However, this function primarily finds wider applicability in signal analysis and related fields. Hence, why the function at 0 is defined to be that limiting value. If you merely interested in wheter or not the integral from zero to infinty exists (is bounded) rather than needing to know it's presice value then this is a much easier problem. F(x) = integral of f(t)dt for t=0 to x.
Observe that f is analytic on the contour and within the domain enclosed by it, so by cauchy's theorem its integral equals zero.
Series expansion of the integral at x=0. The integrals are evaluated by the methods of complex analysis. The laplace transform of sin(x) one of the great workhorses of mathematics is the laplace transform of the function x 7!sin(x): So the integral is undefined.
More rigorously, the integral of f(x) from x=0 to infinity is defined to be the limit at infinity of the function.
We present here this evaluation method using several specific examples. So evaluating pi to any number of digits is easier problem. I = ∫ 0 π sin. (residue theorem) say that c ∼ 0 in r, so that c = ∂s with the bounded region s contained in r.suppose.
The integral of ln(x+1)/(x^2+1) dx from 0 to 1we can use the result from the previous to solve a classical integral we may first, of symmetry reasons, rewrite it as there is several ways to.
The definite integral of sinx from 0 to pi. Dx =0 +∞ −∞ sinx x dx = π (we have omitted the “pv” in the final integral because sinx x is actually finite at x =0.) type 5 integrals our last type of integral will be those involving branch cuts. In this section we’ve got the proof of several of the properties we saw in the integrals chapter as well as a couple from the applications of integrals chapter. Newton did it by integrating a quarter circle to get the area = pi/4.
Type of integrals under conditions where the curve partially lies at infinity, one makes use of complex variable methods and in particular the cauchy integral theorem.
Then the residue of f(z) at z0 is the integral res(z0) =1 2πi z cδ(z0) f(z)dz. In this tutorial we shall derive the definite integral of the trigonometric function sine from limits 0 to pi. For the integral from 0 to infinity that you specifically request the value is pi/2, though i dont remember how to do it. First we evaluate this integration by using the integral formula ∫ sin.
\int_{0}^{\infty}\frac{\sin^2 x}{x^2}dx = \frac{\pi}{2} $$.
Res z = 0 ( f) = lim z → 0 z f ( z) = e 0 = 1. We're going to use the lemma, and in particular its corolary, that in the first and most upvoted answer here. The integration of the form is. In this video, i calculate the integral of sin(x^n) from 0 to infinity, without using any complex analysis whatsoever.
Complex integration 1.3.2 the residue calculus say that f(z) has an isolated singularity at z0.let cδ(z0) be a circle about z0 that contains no other singularity.
Far from being a problem, these can actually make some kinds of definite integral possible because we