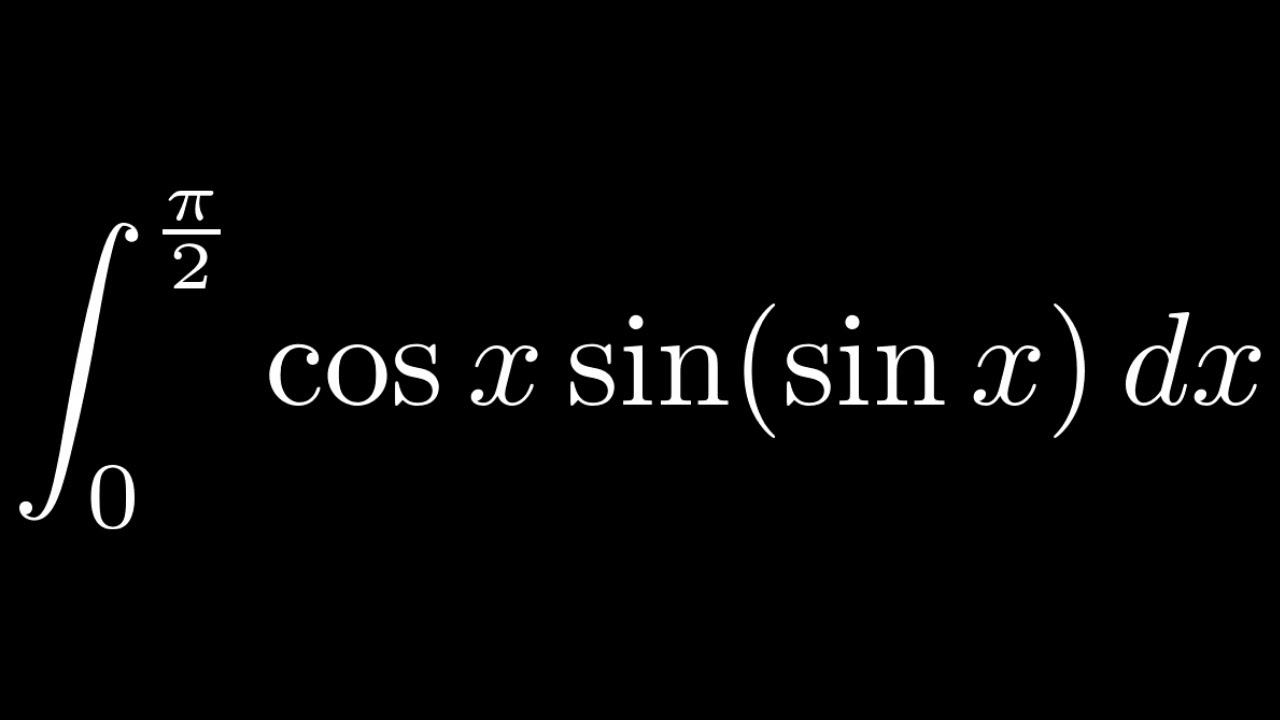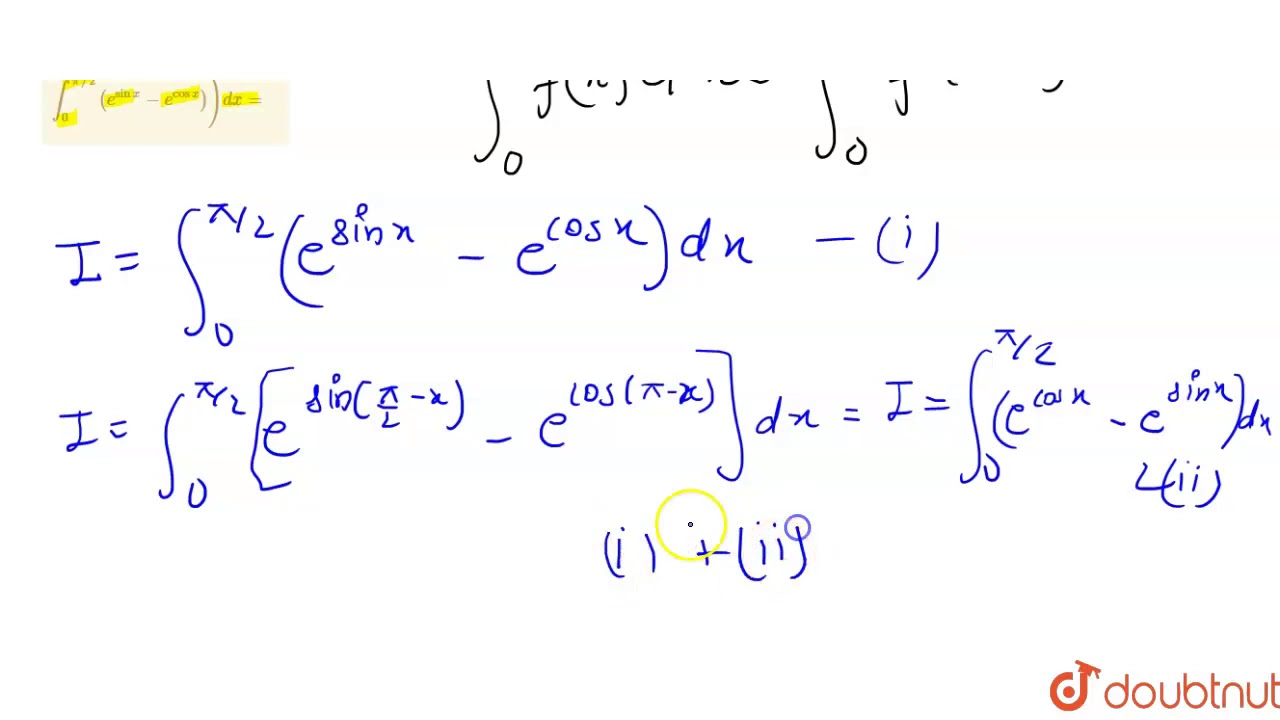Integral Of Sinx Cosx From 0 To Pi `int_()^(pi//2) (sinx )/(sin X + Cos X ) Dx=` YouTube

The integration of the form is. Evaluate integral from 0 to pi/4 of sin (x) with respect to x. Find the integration from 0 to pi/2 of[xsinx cosx/sin 4 x + cos 4 x] find the integration from 0 to pi/2 of.

Definite Integral of cos(x)sin(sin(x)) from 0 to pi/2

∫ π 0 max (cosx,sinx)dx = ∫ π 4 0 cosxdx +∫ π π 4 sinxdx = 1 + √2.

∫ 0 π / 2 1 1 + cos ⁡ x + sin ⁡ x d x.

A unique platform where students can interact with teachers/experts/students to get solutions to their queries. And so you have that. Where each integral is over the limits [0, [itex]\pi[/itex]/2], for a 'well behaved' function f. On adding both the integrals,

The definite integral of sinx from 0 to pi.

Integral from 0 to pi of sin (x) \square! In this tutorial we shall derive the definite integral of the trigonometric function sine from limits 0 to pi. I = ∫ 0 π cos. Students (upto class 10+2) preparing for all government exams, cbse board exam, icse board exam, state board exam, jee (mains+advance) and neet can ask questions from any subject and get quick answers by.

First we evaluate this integration by using the integral formula ∫ sin.

X] we will notify on your mail & mobile when someone answers this question. Comapring the coefficient od sin. 22430 views around the world you can reuse this answer creative commons license Misc 30 evaluate the definite integral ∫_0^ (𝜋/4) 〖 (sin⁡𝑥 + cos⁡𝑥)/ (9 + 16 sin⁡2𝑥 ) 〗 𝑑𝑥 ∫_0^ (𝜋/4) 〖 (sin⁡𝑥 + cos⁡𝑥)/ (9 +16 sin⁡2𝑥 ) 〗 𝑑𝑥 let sin⁡𝑥−cos⁡𝑥=𝑡 differentiating both sides 𝑤.𝑟.𝑡.𝑥 cos⁡𝑥+sin⁡𝑥=𝑑𝑡/𝑑𝑥 𝑑𝑥=𝑑𝑡/ (sin.

Use math input mode to directly enter textbook math notation.

Thanks for watching my vodeo, today we are going to discuss definite integral of {sqrt(sinx)/[sqrt(sinx)+sqrt(cosx)]}dx from 0 to pi/2. In this tutorial we shall derive the definite integral of the trigonometric function cosine from limits 0 to pi. The definite integral of cosx from 0 to pi. The attempt at a solution i have tried relating sin(x) and cos(x) and somehow rearrange one of the integrals to look like the other.

The integration of the form is.

Thus you need to compute. Which can be done with the substitution t = tan ⁡ ( x / 2), that yields. Extra close brace or missing open brace. Which indeed shows that $\int_{0}^{\pi} \sin(2x) dx$ is odd about $\pi / 2$ giving the value of original integral as $0$.

Let i = ∫ 0 π 2 cos x 3 cos x + sin x ⋅ d x.

Extra close brace or missing open brace. I = ∫ 0 π sin. X d x = sin. Jim h · mason m.

Integral from 0 to π/2 {[x sin x cos x] / [cos^(4) x + sin^(4) x]}dx =

Π 2 = ∫ 0 π / 2 1 + cos ⁡ x + sin ⁡ x 1 + cos ⁡ x + sin ⁡ x d x = ∫ 0 π / 2 1 1 + cos ⁡ x + sin ⁡ x d x + 2 i. ∫ π 4 0 sin (x) dx ∫ 0 π 4 sin ( x) d x. Your first 5 questions are on us!

integrate sin^2x / (sinx + cosx) limit 0 to Pie/2

Integrate sinxcosx/sinx +cosx Maths Integrals

Find the integral of x*sin2x*sin [(PI/2)*cosx ] / (2x PI

Evaluate `int_0^(pi/2) ((xpi/4)^2 sinx)/(sinx+cosx)dx

The value of the integral `int_(0)^(pi//4) (sinx+cosx)/(3

`int_(0)^(pi//2) cosx\\ e^(sinx)\\ dx` is equal to YouTube

integrate 0 to (pi)/2 {(x+sinx)/(1+cosx)} Maths