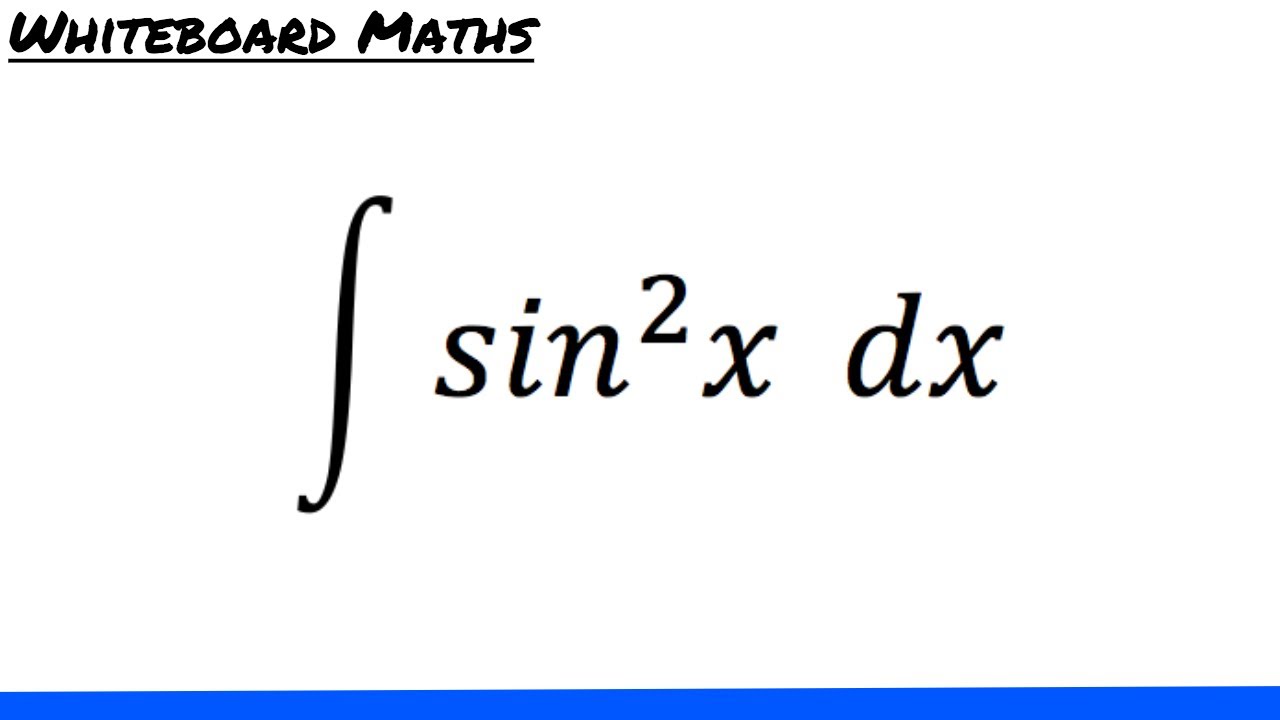\[\int \sin^{2}x \, dx\] +. Follow this answer to receive notifications. Rewrite using u u and d d u u.
Solved Integral Sin^2(theta) Cos^2(theta)d Theta =integra
Integrate 1/(cos(x)+2) from 0 to 2pi;
So sin2a = 1 − cos2a 2.
Let u = 2 θ u = 2 θ. = 1 6 (3x − 1 2 sin(2 ⋅ 3x)) + c. X^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le. Then we use the cosine double angle formulae.
Well, since thw op hasn't shown up yet, i am going to make it a little bit easier for him.
How to integrate sin^2 x using the addition formula for cos(2x) and a trigonometric identity. I = ∫ sin 2 x d x. = 1 2 x − 1 12sin6x + c. The integration is of the form.
So that will be your answer.
Here are some examples illustrating how to ask for an integral. Since 1 2 1 2 is constant with respect to θ. Let us first simplify sin 2 x, using the trigonometric identity. \rightarrow {r^2}\left( {{{\cos }^2}\theta + {\sin^2}\theta } \right) = 2r\cos \theta ,\;\;
∫ sin(2θ 3)dθ ∫ sin.
( 2 θ 3) d θ. Evaluate the integral sin^2(2 theta) d(theta) from theta=0 to pi/2 \rightarrow r = 2\cos \theta.\] Go through the explanation to understand better.
Then du = (2θ 3)′ dθ = 2dθ 3 d u = ( 2 θ 3) ′ d θ = 2 d θ 3 and we have that dθ= 3du 2 d θ.
So now this is equal to 1/2 day to minus 1/4 sine two theta and then pussy. Θ + 1 = csc 2. Integral from 0 to (pi)/2 of sin^2 (theta)cos^2 (theta)heta. Int cos(2theta) dtheta = 1/2 sin(2theta) + c, where c is an integration constant.
Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals.
Find d u d θ d u d θ. Cos2a = 1 − 2sin2a. And then don't forget to r plus c at the end. Find the integral sin (2theta) sin(2θ) sin ( 2 θ) let u = 2θ u = 2 θ.
Evaluate integral of sin (theta)^2 with respect to theta.
∫ sin2 (θ)dθ ∫ sin 2 ( θ) d θ. Like cristo suggested you need to write sin (theta) in terms of sin (theta/2) notice that sin (theta)=sin (2 (theta/2)), now applying the double angle forumula for sin, what do we get?? The integral of coast tooth data is going to be signed to data but we need a one half in the front to cancel out with the changeable. \underline{\mathbf{\text{first solution}}} \displaystyle\int \sin\,\theta\cos\,\theta\,d\theta = \dfrac{1}{2}\sin^2\,\theta + c \quad \displaystyle.
Substituting the expressions \(x = r\cos \theta ,\) \(y = r\sin \theta ,\) we obtain the equation of the circle in polar coordinates.
Now, split the integrals such that the heavyside theta function is well separated. Extended keyboard examples upload random. I = ∫ − l / 2 l / 2 d x θ ( ϵ − 2 a | x |) = ∫ − l / 2 0 d x θ ( ϵ − 2 a | x |) + ∫ 0 l / 2 d x θ ( ϵ − 2 a | x |) = ∫ − l / 2 0 d x θ ( ϵ + 2 a x) + ∫ 0 l / 2 d x θ ( ϵ − 2 a x). Cos2θ= 1+cos(2θ) 2 cosθsinθ= sin(2θ) 2 sin2θ= 1−cos(2θ) 2.
Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;
\[{x^2} + {y^2} = 2x,\;\; I think you mean cos(2theta) instead of cos2(theta). Let u = 2θ 3 u = 2 θ 3. Let u = 2theta, frac{du}{dtheta} = 2.
For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music…
= 1 6 (u − 1 2sin2u) + c. \rightarrow {r^2}{\cos ^2}\theta + {r^2}{\sin^2}\theta = 2r\cos \theta ,\;\; What is the integral of sin 2 theta? = 1 6 ∫ 1 −cos2u du.
Like sin (x+y) = sin (x)cos (y)+cos (x)sin (y), now apply the same.
The value of the integral \(\int\frac{sin\theta. If you know that int cos(x) dx = sin(x) + c, then we can use a substitution (which is the reverse of the chain rule). Set u = 2x and du = 2dx to perform u substitution on the integral. Then du = 2dθ d u = 2 d θ, so 1 2du = dθ 1 2 d u = d θ.
To avoid ambiguous queries, make sure to use parentheses where necessary.