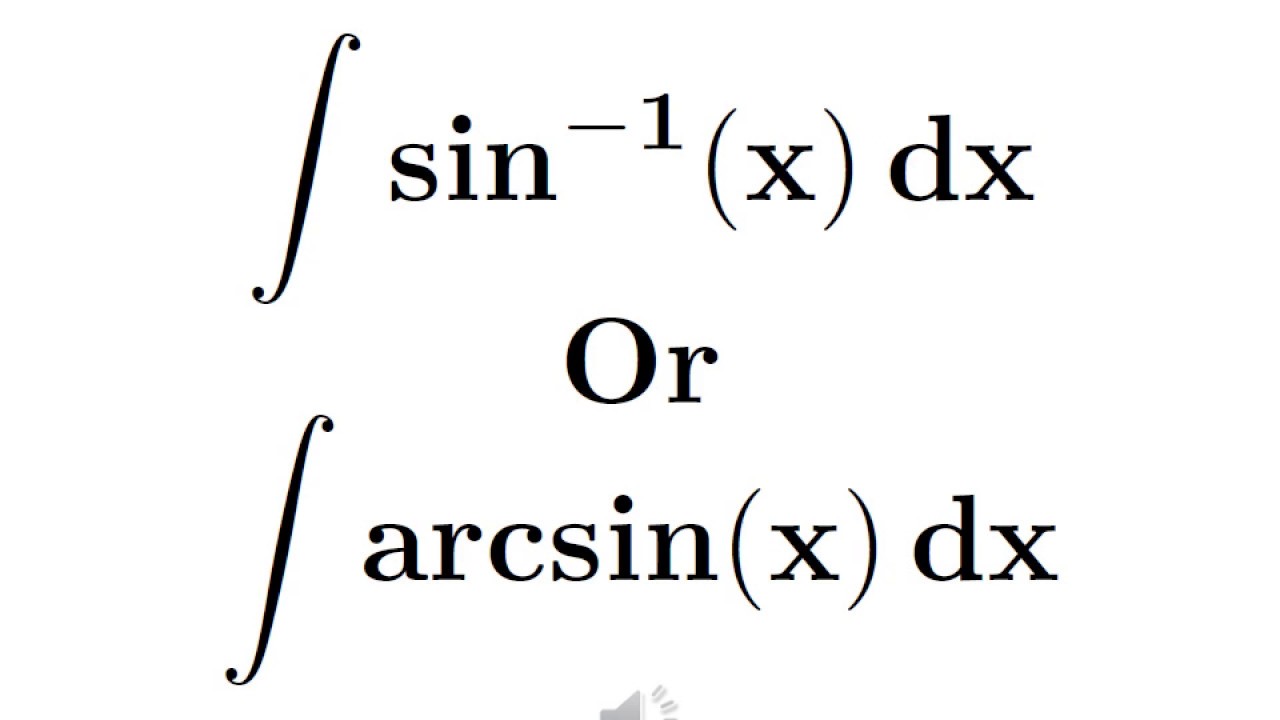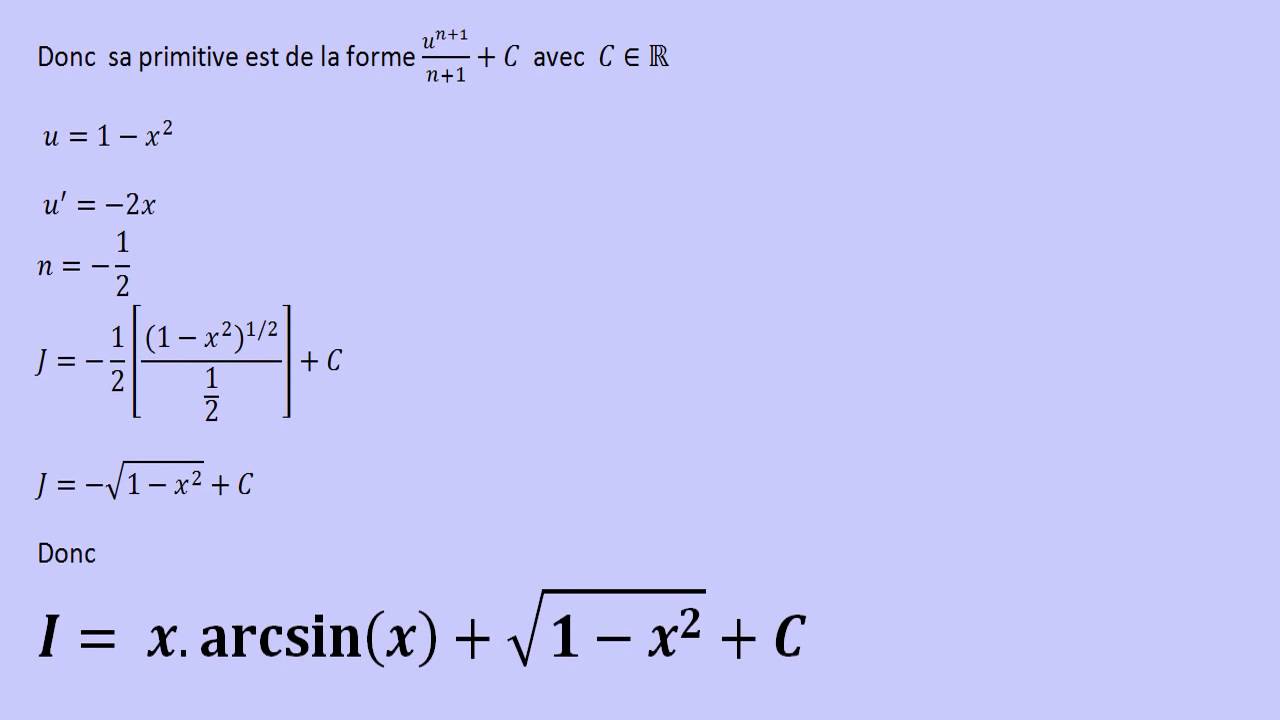Therefore, the integral of sin4x dx = (3/8)x + (1/32) sin (4x) − (1/4) sin (2x) + c. Naveen sharma 4 years, 6 months ago. On simplifying the above expression, we get.
Example 43 Evaluate integral x sin (pi x) dx Examples
Let u = t and d v = sin.
= ∫ 2 x d x = 2 x 2 2 + c = x 2 + c.
= ∫ s i n − 1 ( s i n 2 x) d x. We can use integration by parts. ∫ sin−1x dx= xsin−1x+√1−x2+c 1. ∫ s i n − 1 ( 2 t a n x 1 + t a n 2 x) d x.
Ex 7.6, 10 (sin^ (−1)𝑥 )^2 ∫1 (sin^ (−1)𝑥 )^2 𝑑𝑥 let sin^ (−1)𝑥=𝜃 ∴ 𝑥=sin𝜃 differentiating both sides 𝑤.𝑟.𝑡.𝑥 𝑑𝑥/𝑑𝜃=cos𝜃 𝑑𝑥=cos𝜃.𝑑𝜃 thus, our equation becomes ∫1 (sin^ (−1)𝑥 )^2 𝑑𝑥 = ∫1 𝜃^2.
The indefinite integral of , denoted , is defined to be the antiderivative of. The integration of sine inverse is of the form. Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi; Integration of sin inverse can be done using different methods such as integration by parts and substitution method followed by integration by parts.
Area left of x = siny and right of y axis from y = 0 to y = π 2 is:
Cos𝜃.𝑑𝜃 =𝜃^2 ∫1 〖cos𝜃.𝑑𝜃〗−∫1 (𝑑 (𝜃^2 )/𝑑𝜃 ∫1 〖cos𝜃.𝑑𝜃〗)𝑑𝜃 =𝜃^2 sin𝜃−∫1 〖2𝜃.sin𝜃. Now, integrate the function, we get. Get the answer to this question and access a vast question bank that is tailored for students. Integral of sin inverse x is also called the antiderivative of sin inverse x.
X + 1 − x 2 + c.
The integral of x sine inverse of x is of the form. Integration of inverse trigonometric functions. Okay, so what do we do instead? Area of rectangle minus area left of x = siny and right of y axis from y = 0 to y = π 2.
Where c is the integration constant.
Integration of sin inverse x. X d x = x sin − 1. Integration is an important tool in calculus that can give an antiderivative or represent area under a curve. Area of rectangle = base x height = 1 × π 2 = π 2.
Integration of sin inverse x.
Tan(x^2)=m dx=cos(x^2)dm integral [sin(x^2)] = integral [mdm/(m^2+1)] m^2+1=a and 2mdm=da. Then, use integration by parts. Use the substitution t = x, and then use integration by parts. Let i = \displaystyle \int \arcsin(\sqrt{x}) \, \mathrm{d}x \tag*{} you might be tempted to make a substitution like \sqrt{x}= \sin(u) to get rid of the \arcsin term but this probably isn’t the best approach.
X d x = 2 ∫ t sin.
When using integration by parts it must have at least two functions, however this has only one function: ∫ π 2 0 sinydy = − cosy]π 2 0 = −0 −( −1) =. = (3/8)x + (1/32) sin (4x) − (1/4) sin (2x) + c. I1 = 1/2 ∫1 〖〖−𝑥〗^2/( −√(1 − 𝑥^2 )) 𝑑𝑥〗 i1 = (−1)/2 ∫1 〖〖−𝑥〗^2/( √(1 − 𝑥^2 )) 𝑑𝑥〗 i1 =(−1)/2 ∫1 〖〖−1 + 1 − 𝑥〗^2/( √(1 − 𝑥^2 )) 𝑑𝑥〗 (adding and subtracting 1 in numerator ) i1 = (−1)/2 ∫1 〖((−1)/√(1 − 𝑥^2 )+(1 −〖 𝑥〗^2)/√(1 − 𝑥^2 )) 𝑑𝑥〗 i1 = (−1)/2 (∫1.
We have, i = ∫ x s i n − 1 x dx.