We recall the pythagorean trig identity and rearrange it for the cosx squared term. Here, we use the power reduction formula to integrate sin 4 x. Let, i = ∫ sin 4 x dx.
Calculus Archive November 21, 2014
= 1 3 cos3(x) +c.
We factorise out one of the cosx terms to get a cosx squared term.
Integrating the third power of \sin (x) (or any odd power, for that matter), is an easy task (unlike ∫ \sin^2 (x)\,dx, which requires a little trick). $x$ squared and $x$ cubed are two power functions but the cube of $x$ represents an angle inside the sine function. Let u = cos(x) ⇒ du = − sin(x)dx. To do so, we will use the cos2x formula in terms of sine only.
To integrate cos^3x, also written as ∫cos 3 x dx, cos cubed x, cos^3 (x), and (cos x)^3, we start by using standard trig identities to simplify the integral.
Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi; Also, we can write sin 4 x = (sin 2 x) 2. = u3 3 + c. The indefinite integral of three times the product of $x$ squared and sine of angle $x$ cubed with respect to $x$ is written as follows.
∫ e x d x = e x + c \int e^x \;dx = e^x+c ∫exdx=ex+c.
Sin^2𝑥 cos^3 𝑥〗 𝑑𝑥 =∫1 〖𝑠𝑖𝑛𝑥 (1−cos^2𝑥 ) cos^3 𝑥〗 𝑑𝑥 =∫1 〖(1−cos^2𝑥 ) cos^3 𝑥〗. Let cos α + cot x s i n α = t ⇒ − c o sec 2 x sin α d x = d t ∴ ∫ sin 3 x sin ( x + α ) 1 d x = ∫ cos α + cot x sin α c o sec 2 x d x = sin α − 1 ∫ t d t If someone show me step by step solution i would really. = 1/2 e^x x^2 sin(x).
I need to calculate the following integral for my homework, but i dont know how.
Integrate 1/(cos(x)+2) from 0 to 2pi; As you can see, it means the same thing. In this section, we will evaluate the integral of sin^4x (that is, sin 4 x). For the second integral, using substitution:
Here are some examples illustrating how to ask for an integral.
Putting it all together, we get our final result: ∫ 1 x d x = ln x + c \int {1\over x} \;dx= \ln x+c ∫x1dx=lnx+c. To avoid ambiguous queries, make sure to use parentheses where necessary. X 𝑑(cos𝛼 + cot𝑥 sin𝛼 )/𝑑𝑥=𝑑𝑡/𝑑𝑥 𝑑(cos𝛼 )/𝑑𝑥+sin𝛼 𝑑(cot𝑥 )/𝑑𝑥=𝑑𝑡/𝑑𝑥 =∫1 〖1/√(sin^4𝑥 )×1/√(cos𝛼 + cot𝑥.
∫ a x d x = a x ln a + c \int a^x \;dx= {a^x\over \ln a}+c ∫axdx=lnaax+c.
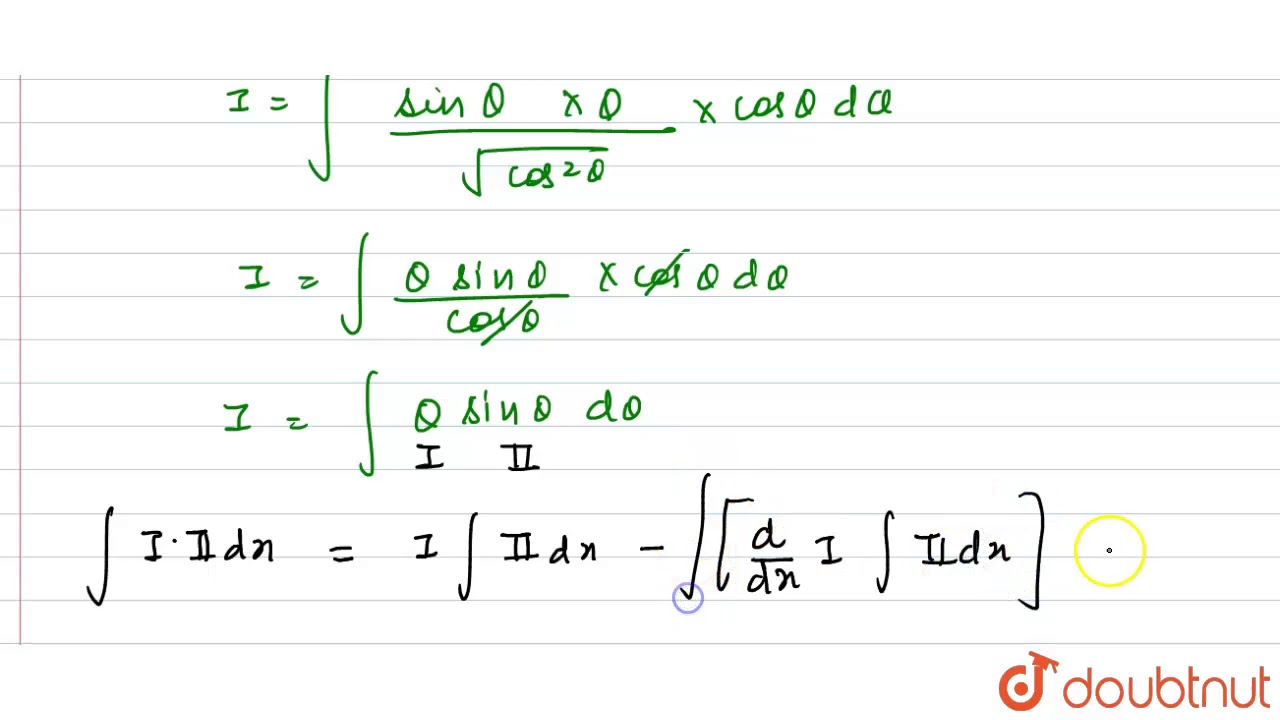
![[IIT 1984] Find dy/dx if y = exp{x*sin[cube(x)]} + (tanx](https://i.ytimg.com/vi/4vAaIzWI2mw/maxresdefault.jpg)


![[最も人気のある!] integral de tan^2 x 189928Integral de tan^2 x dx](https://i2.wp.com/useruploads.socratic.org/hUsCWV2TS2zF0fAQwPl0_Int1_1.jpg)
