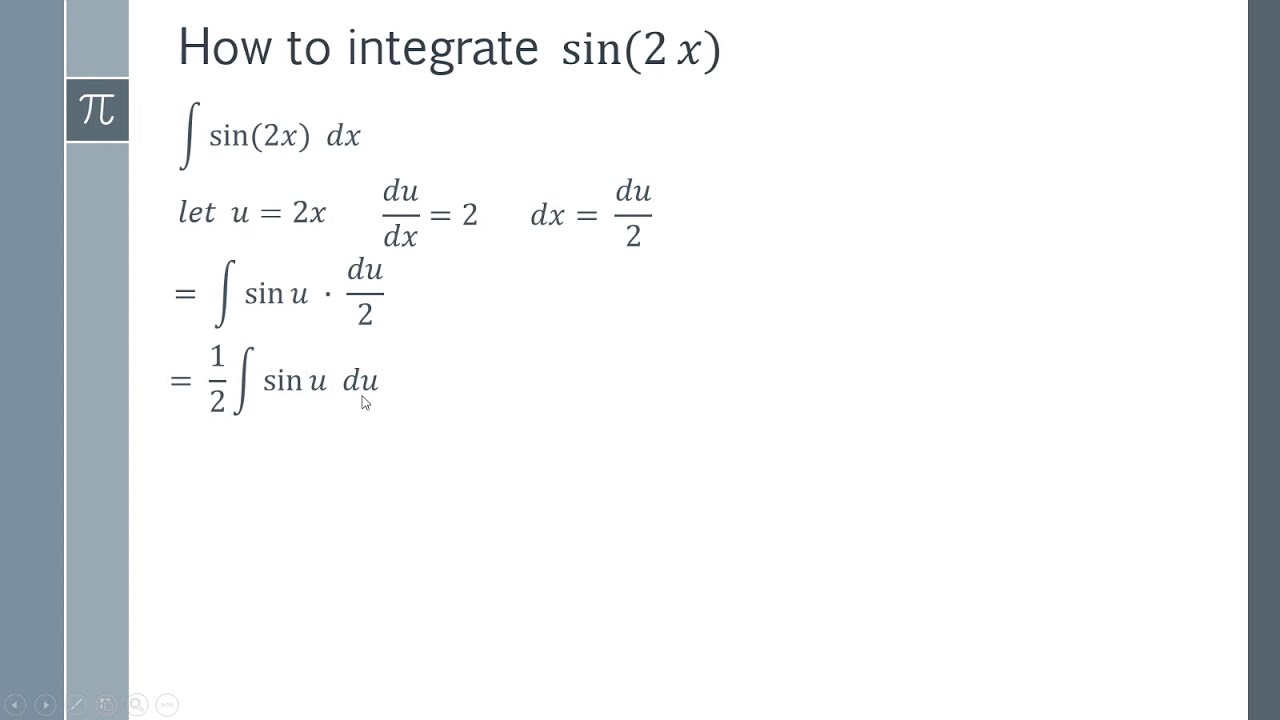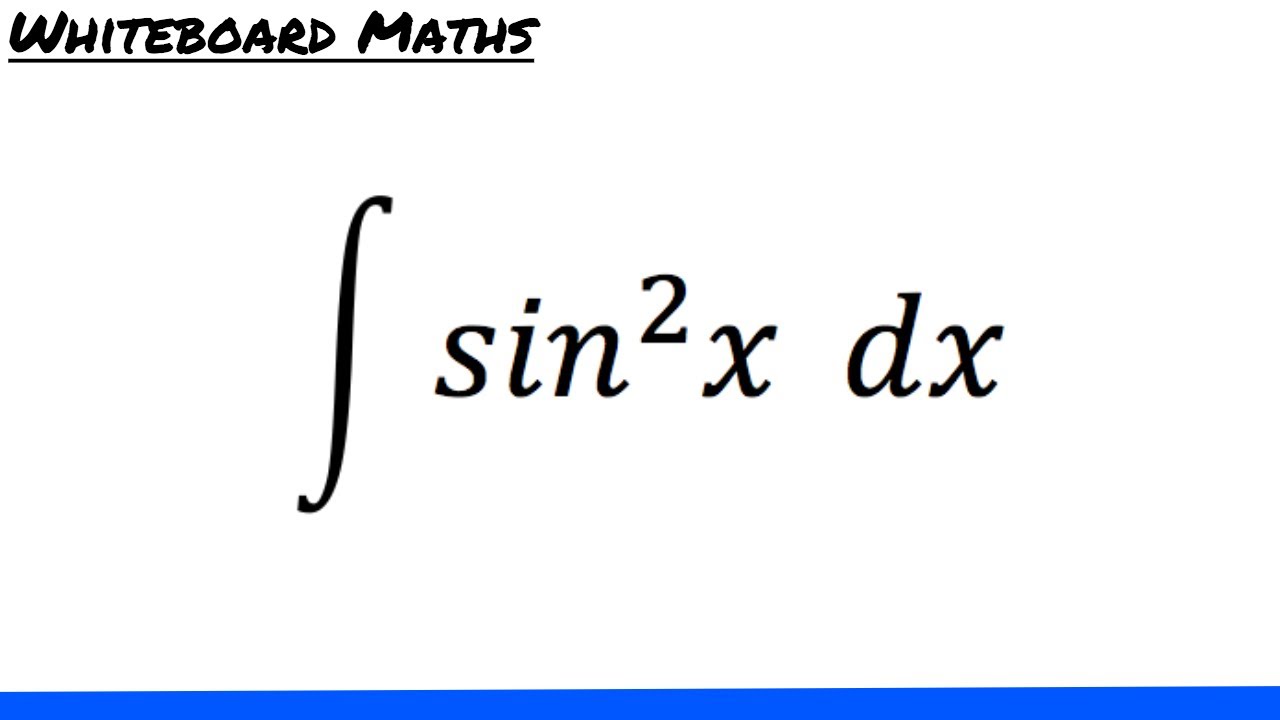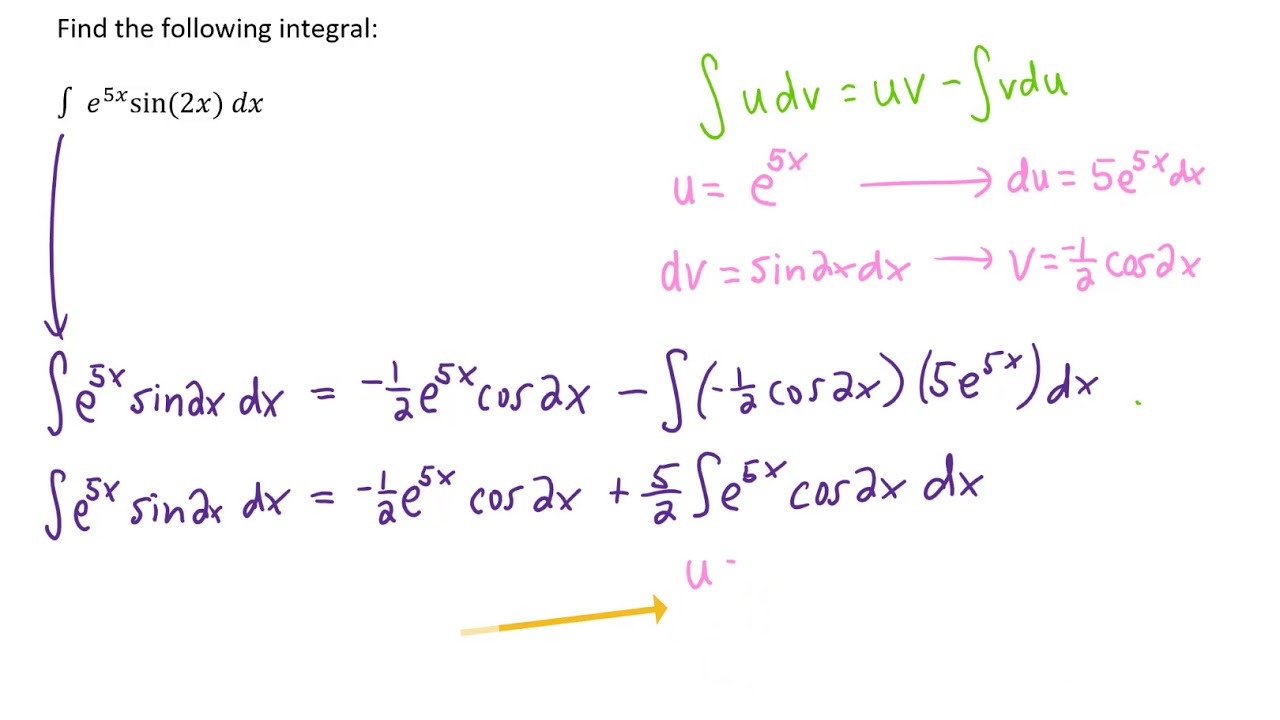2 2 i = 1 2. Evaluate integral of e^ (2x)sin (2x) with respect to x. Then du = 2dx d u = 2 d x, so 1 2du = dx 1 2 d u = d x.
Integral of x sin(2x^2) YouTube
If we apply integration by parts to the rightmost expression again, we will get ∫\sin^2 (x)dx = ∫\sin^2 (x)dx, which is not very useful.
Integrate 1/ (cos (x)+2) from 0 to 2pi.
To prove this, we use the substitution method. For this, assume that 2x = u. Here are some examples illustrating how to ask for an integral. Apply integration by parts for second part and you will get the required answer.
Rewrite using u u and d d u u.
For sin 2 (x), we will use the cos double angle formula: Sin4(2x) = 3 8 − cos(4x) 2 + cos(8x) 8. The integral of cos 2x dx is denoted by ∫ cos 2x dx and its value is (sin 2x) / 2 + c, where 'c' is the integration constant. Answered nov 15, 2018 by shrutibharti (34.5k points) selected nov 15, 2018 by faiz.
Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi.
Evaluate the following integrals : Let’s write \sin^2 (x) as \sin (x)\sin (x) and apply this formula: Since 1 2 1 2 is constant with respect to x x, move 1 2 1 2 out of the integral. ∫ e2x sin(2x)dx ∫ e 2 x sin ( 2 x) d x.
The integral of the trigonometric function is (1/2)(e^(sin 2x)) + c.
Sin2(2x) = 1 2 ⋅ (1 − cos(4x)) hence we have that. ∫sin4(2x)dx = 3 8∫dx − 1 2∫cos(4x)dx + 1 8∫cos(8x)dx. Find d u d x d u d x. ( x) + sin 2.
( x) = 1 and do the appropriate change of variable.
Let u = 2 x u = 2 x. Let u = 2 x u = 2 x. Inverse trigonometric integrals and integration by parts homework evaluate each of the following integrals. We just have to keep applying integration by parts here until all we have left is a trig function.
Using the linearity of the integral:
The first integral is easy, and the last two can be evaluated by changing the variable to u = cos(x) : Let u = 2x u = 2 x. First we choose u = x3 u = x 3 and dv= sin2x dx d v = sin. Find d u d x d u d x.
Share it on facebook twitter email.
Then du = 2dx d u = 2 d x, so 1 2du = dx 1 2 d u = d x. We know that, 2 sin a cos b = sin (a + b) + sin (a − b) so, ∫ sin 2 x cos 3 x d x = 2 1 ∫ [ 2 sin 2 x cos 3 x ] d x = 2 1 ∫ [ sin ( 2 x + 3 x ) + sin ( 2 x − 3 x ) ] d x = 2 1 ∫ [ sin 5 x + sin ( − x ) ] d x = 2 1 ∫ [ sin 5 x − sin x ] d x [ ∵ sin ( − θ ) = − sin θ ] = 2 1 ∫ sin 5 x d x − 2 1 ∫ sin x d x = 1 0 1 ( − cos 5 x ) + 2 1 cos x = 2 1 cos x − 1 0 1 cos 5 x. ∫sin4(2x)dx = 3x 8 − 1 8 ∫cos(4x)d(4x) + 1 64∫cos(8x)d(8x) ∫sin4(2x)dx = 3x 8 − sin(4x) 8 + sin(8x) 64 +c. ∫dx/(sin x + sin 2x) integrals;
This is the general method to integrate functions of the type.
Share it on facebook twitter email. Answered jan 27, 2020 by rubby01 (50.3k points) selected jan 30, 2020 by pankaj01. ∫sin2(2x)dx = ∫[1 2 ⋅ (1 − cos(4x))]dx = x 2 − sin(4x) 8 +c. Let u = 2x u = 2 x.
We have to integrate of sin 2 x.
2 i = sin 2 sin 2 i = sin. What is the integral of cos 2x e^(sin 2x) dx? Then 2 dx = du (or) dx = du/2. Rewrite using u u and d d u u.