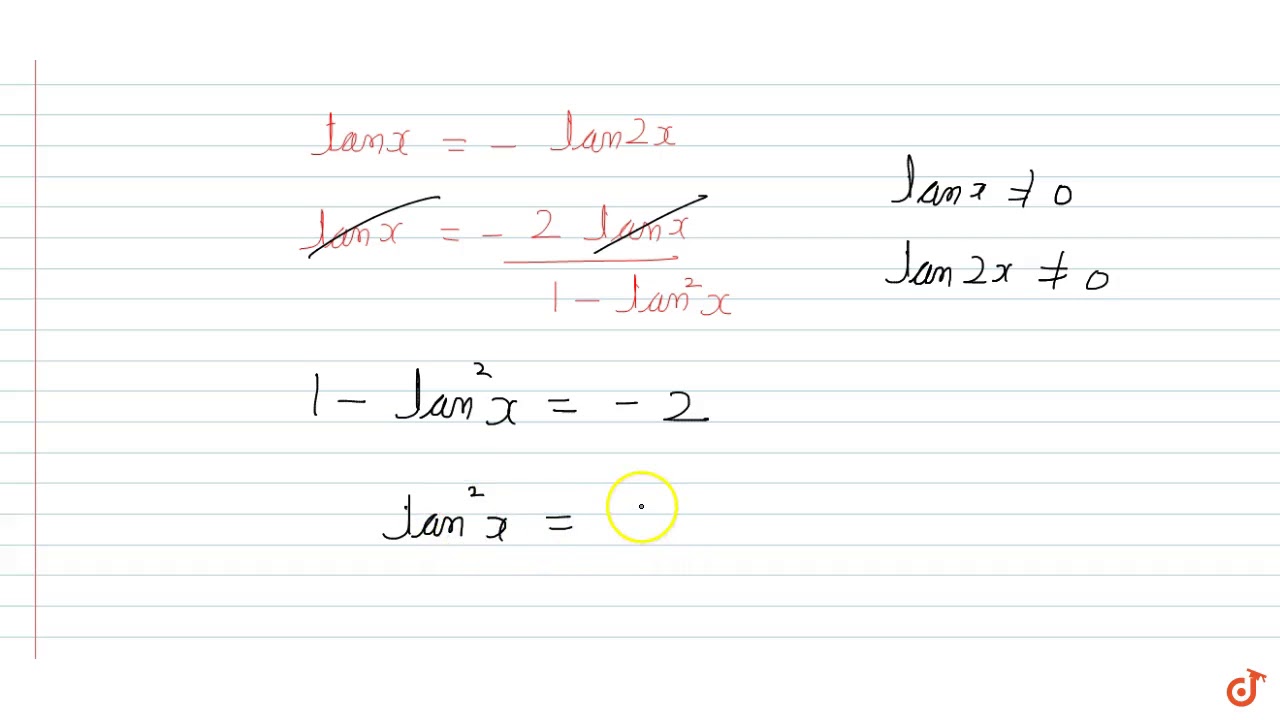So integral convert into ∫ t. Ex 7.2, 35 → chapter 7 class 12 integrals (term 2) serial order wise; ⇒ sec 2 x dx = 2t dt.
The general solution of the equation `tanx/tan(2x)+tan(2x
1 2 tanx dx take u.
We think that the integrand of i has the other factor 1 and integrate partially:
⇒ dx = [2t / (1 + t 4 )]dt. A unique platform where students can interact with teachers/experts/students to get solutions to their queries. So integral is 2 ∫ t 2. ( 1 − t 4) − 1 2 d t.
Which is integrable only when ( m + 1 n) ∈ z or { m + 1 n + p } ∈ z.
Integration of the square root of a^2+x^2. Sometimes when faced with an integral that contains a root we can use the following substitution to simplify the integral into a form that can be easily worked with. (a) √ (tan x) + c. Let tan x = t 2.
X d x = 2 t d t ⇔ d x = 2 t 1 − t 4 d t.
This states that if is continuous on and is its continuous indefinite integral, then. Example 42 important → chapter 7 class 12 integrals (term 2) serial order wise; The answer is =2sqrt(tanx)+c we need tanx=sinx/cosx sinx=cosxtanx=tanx/secx therefore, the integral is i=int(sqrt(tanx)dx)/(sinxcosx)=int(sqrt(tanx)dx)/(tanx/secx*1/secx) =int(sec^2xdx)/sqrt(tanx) let u=tanx, =>, du=sec^2xdx the integral is i=int(du)sqrt(u) =sqrt(u)/(1/2) =2sqrt(u) =2sqrt(tanx)+c We have i = ∫ 2 tanx sin 2 x dx = ∫ 2 tanx cosec 2 x dx take cosec 2 x = 1 2 cosx sinx, sinx = tanx secx, cosx = 1 secx i = 2 ∫ sec 2 x.
Students (upto class 10+2) preparing for all government exams, cbse board exam, icse board exam, state board exam, jee (mains+advance) and neet can ask questions from any subject and get quick answers by.
What i was really after was how you would integrate the original function algebraically. Now using ∙ ∫ x m. Lovina kansal, meritnation expert added an answer, on 28/12/16. ⇒ sec 2 x dx = 2t dt.
We are going start multiplying by a creative form of one, using a conjugate.
∫ √tanx sin2x dx ∫ t a n x s i n 2 x d x is. Both types of integrals are tied together by the fundamental theorem of calculus. The definite integral of from to , denoted , is defined to be the signed area between and the axis, from to. If the question is asking for an indefinite integral of, i.e., an antiderivative for, the function \sqrt{\sin{(2x)}}, to my knowledge such does not exist in terms of elementary functions.
Let’s do a little rewriting first.
(c) (1/2) √ (tan x) + c. Integral of sqrt(tan(x))/sin(2x)don’t forget to subscribe before you watch my next video = )blackpenredpen (b) 2√ (tan x) + c. ⇒ integral ∫ 2t 2 / (1 + t 4) dt.
2 t ( 1 − t 4) 1 2 d t.
Let tan x = t 2. Evaluate the indefinite integral integrate of sin^4(x)cos^4(x)dx. ∫ a 2 + x 2 d x = x a 2 + x 2 2. The integral of a 2 + x 2 is of the form.
This integral can be written as.
(d) (1/4) √ (tan x) + c. ⇒ dx = [2t / (1 + t 4 )]dt. ⇒ integral ∫ 2t 2 / (1 + t 4) dt. Closed oct 8, 2020 by ramankumar.
Sometimes an approximation to a definite integral is.
Where m, n, p are rational no. U = 3 √ x − 3 u = x − 3 3. Integration of sqrt(sin(x)) expert answers. Ex 7.2, 1 ex 7.2, 2 ex 7.2, 3 important.
Ex 7.2, 4 ex 7.2, 5.
Tan(3x)=tan(x+2x)tan(3x)= 1−tanx.tan2xtanx+tan2x tan(3x)−tanx.tan(2x).tan(3x)=tanx+tan(2x)∴tanx.tan(2x).tan(3x)=tan(3x)−tan(x)−tan(2x) ___________ (1)∫tanx.tan(2x).tan(3x).dx=∫tan(3x)−tan(x)−tan(x)−tan(2x).dx (fomi)= 31 log ∣sec(3x)∣−log∣secx∣− 21 log∣sec(2x)∣+c. So, instead of letting u u be the stuff under the radical as we often did in calculus i we let u u be the whole radical. In this tutorial we shall derive the integration of the square root of a^2+x^2, and solve this integration with the help of the integration by parts methods. ( a + b x n) p d x.
Please log in or register to add a comment.
Example 1 (i) example 1 (ii) example 1 (iii) example 2 (i).