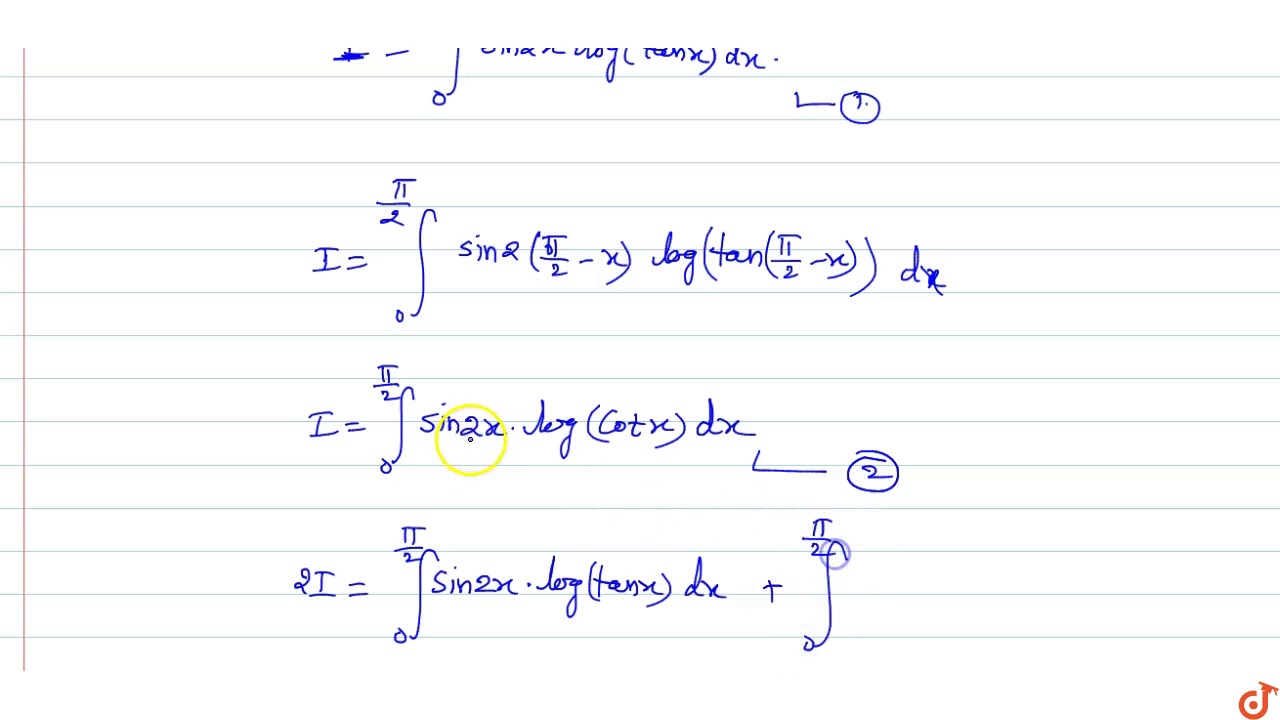Int_0^pi tanx dx is convergent and int_0^pi tanx dx = 0 tan x has a discontinuity when x=pi/2 so for a thorough robust solution we would need to split the integral as follows; Inform you about new question papers. The value of the integral ∫ limits0(π/2) log (tan x)dx= (a) 0 (b) 1 (c) (π/2) (d) (π/4).
Putnam Exam Integral Integral of 1/(1+tanx^sqrt(2)) from 0
This is easy but very important definite integration 0 to pi/2 log(tanx) || cbse ncert xii state broads ||international students ||#definiteintegration #avte.
The value of the integral ∫ log tan x dx x ∈ [0,π ⁄ 2] is equal to :
∫ 0 π / 2 log. C o t x d x. Ex 7.11, 8 by using the properties of definite integrals, evaluate the integrals : A unique platform where students can interact with teachers/experts/students to get solutions to their queries.
U = ln(z) => du = 1.
( x) d x = − π 2 24. I 1 = 1 2∫ π 0 logsintdt = ∫ π 2 0 logsintdt = i. ∫ 0 π / 2 lo g (tan x + cot x) d x = π (lo g 2) hard. And found this value using the known sum π 2 6.
Why create a profile on shaalaa.com?
Find the answer to this question along with unlimited maths questions and prepare better for jee 2020 exam. By using the properties of definite integrals, evaluate the integral ∫ 0 4. Lata in calculus 1 decade ago, total answer(s): (a) π/4 (b) π/2 (c) 0 (d) π
∫_0^(𝜋/4) log(1+tan𝑥 ) 𝑑𝑥 let i=∫_0^(𝜋/4) log〖 (1+tan𝑥 )〗 𝑑𝑥 ∴ i=∫_0^(𝜋/4) log[1+tan(𝜋/4−𝑥) ] 𝑑𝑥 i=∫_0^(𝜋/4) log[1+(tan 𝜋/4 −tan𝑥)/(1 +〖 tan〗 𝜋/4.
The questions and answers of what is the integration of log (tanx)? Integration of log(1 + tan x) from 0 to pi/4 is equal to π/8 log 2. X d x + ∫ 0 π 2 log. Integrate log(1+tan x) from 0 to pi/4.
There is good reason to do this, even if there is symmetry in the problem.
= ∫ 0 π 2 log. Inform you about time table of exam. I = ∫ 0 π / 2 lo g (tan x + cot x) d x Adding (1) and (2) we get adding (1) and (2) we get.
The result in this case is that the integral does not converge.
Join / login >> class 12 >> maths >> integrals >> properties of definite integrals. Or i = − ( π 2)log2. I would like to see a direct proof of the integral. Tan𝑥 )] 𝑑𝑥 i=∫_0^(𝜋/4) log[1+
2 i = ∫ 0 π 2 log.
Limit is 0 to π/4.? This is an improper integral, and the usual way these are handled is by taking limits at each point of discontinuity (in this case, at $\pi/2$ and $3\pi/2$, from both sides at each). Since, this is a definite integral, to integrate it we have to use the propertiesies of definite integrals. Chapter 7 class 12 integrals (term 2) serial order wise;
Integral 0 to pi/2 of sin 2x log tanx dx.
Although the integral looks horrible at first sight, it's. If the answer is not available please wait for a while and a community member will probably answer this soon. Click here👆to get an answer to your question ️ evaluate: Pioneer, 1 decade ago like.
Are solved by group of students and teacher of class 12, which is also the largest student community of class 12.
Check answer and solution for above mathema Students (upto class 10+2) preparing for all government exams, cbse board exam, icse board exam, state board exam, jee (mains+advance) and neet can ask questions from any subject and get quick answers by. Hence (a) becomes 2i = i −( π 2)log2. I arrived at this integral while trying different ways to evaluate 1 1 2 + 1 2 2 + 1 3 2 +.
In this video, i evaluate the integral from 0 to pi/2 of ln(tan(x)) dx using a simple substitution.
Click here👆to get an answer to your question ️ int0^pi/2log (tan x + cot x)dx = pi (log 2) solve study textbooks guides.