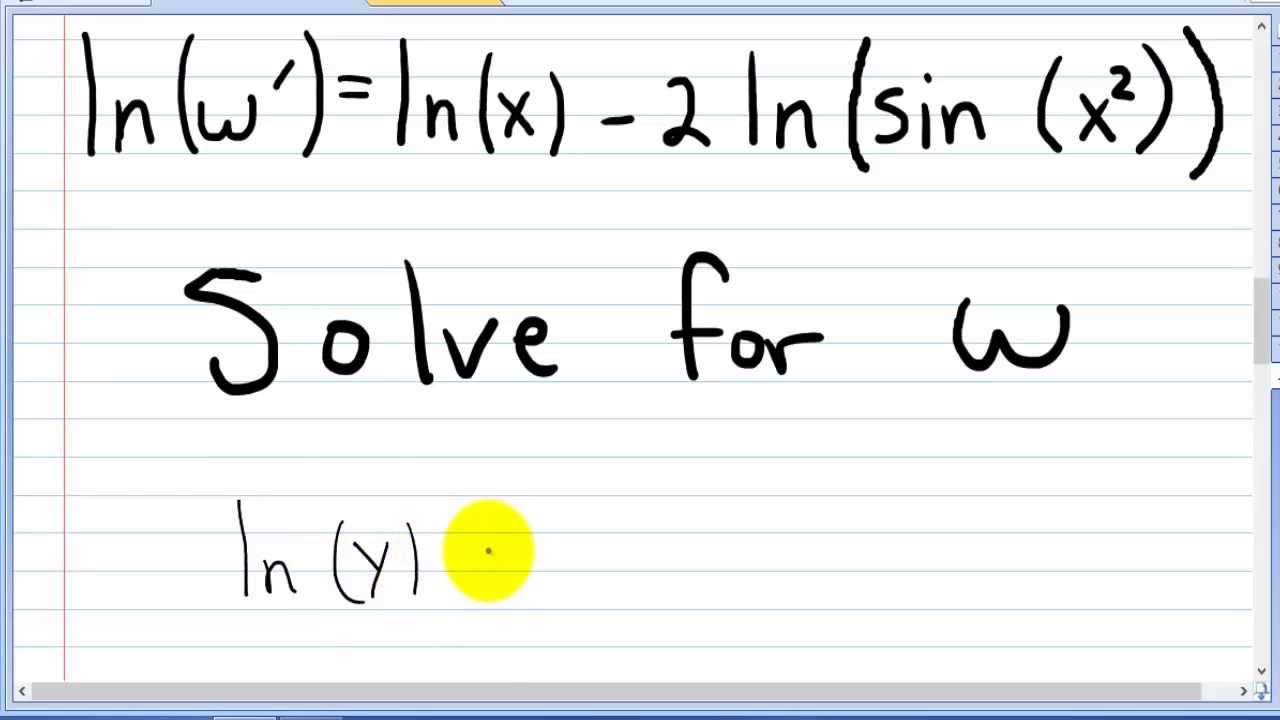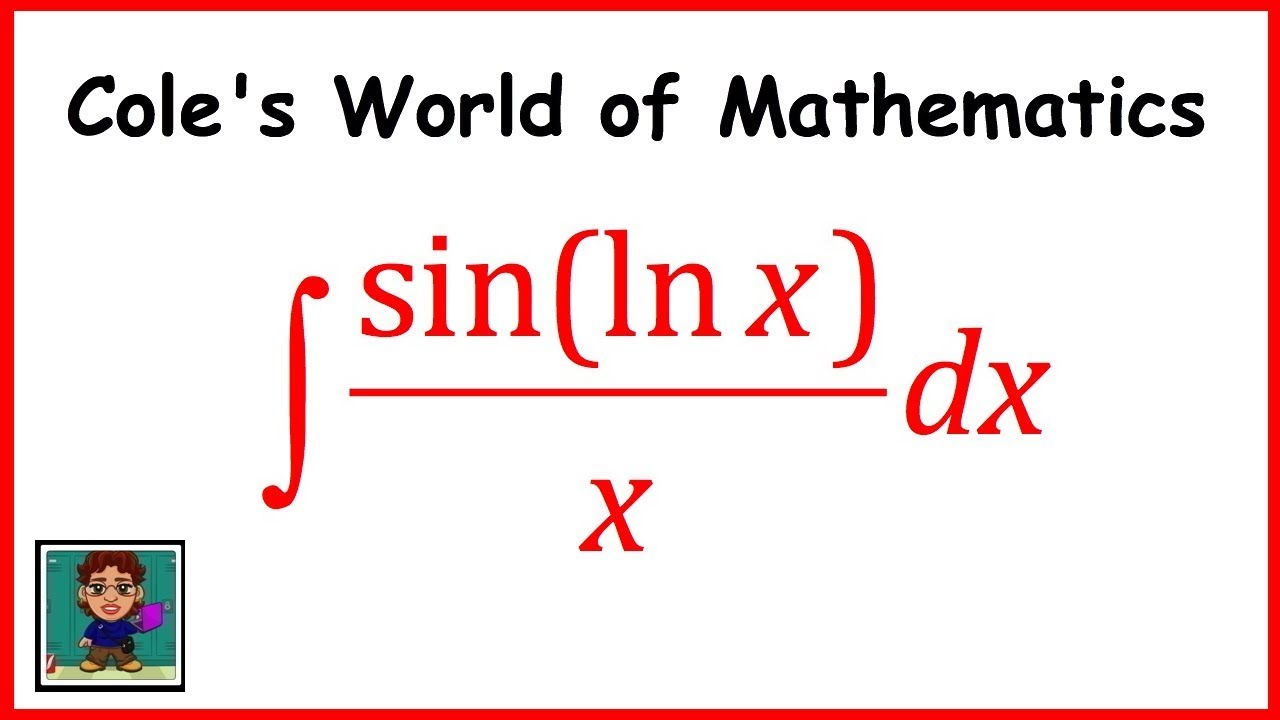It was the improper integral, that i needed to find. Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi; Together these give the reasonably simple bounds:
How to integrate sin(ln x) [Integration by Parts] YouTube
To avoid ambiguous queries, make sure to use parentheses where necessary.
In doing this, the integral calculator has to respect the order of operations.
X^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le. X ⇒ x = e x, then by differentiation d x = e u d u, we have. The integral calculator has to detect these cases and insert the multiplication sign. Sin, cos, tan, ln, exp, sh, th, sqrt (square root), and many others.
Let's call the integral in here i:
S = ∫ π 2 0 ln(sinx)dx. I have to study the convergence of the following integral: Substitute t = π 2 −x. Yaghoub sharifi integration, series february 6, 2018.
We proved here, quite easily, that a more interesting problem is to find (problem 2).
Report thread starter 12 years ago. \bold{\mathrm{basic}} \bold{\alpha\beta\gamma} \bold{\mathrm{ab\gamma}} \bold{\sin\cos} \bold{\ge\div\rightarrow} \bold{\overline{x}\space\mathbb{c}\forall} Integrate 1/(cos(x)+2) from 0 to 2pi; Integral of sin (ln (x)) full pad ».
Actually the definite integral i needed to find is integral {ln (t*cos t) dt.} i think i should be able to do it now with the above help.
2s = ∫ π 2 0 ln(sinx)dx + ∫ π 2 0 ln(cosx)dx. Following the formula for integration by parts, you get x l n (x) − ∫ x x d x the result is that ∫ l n ( x ) d x = x l n ( x ) − x + c it's always good practice to check your answer: Note that, without the application of the chain rule, you can just blindly use the derivative of \ln x and substitute the argument to get \frac{\mathrm{d}y}{\mathrm{d}x} = \frac {1}{1 + \sin 2x},. Suppose that u = ln.
$$\int \sin(u) e^{u} du.$$ integration by parts performed twice, together with the method of solving for the integral, will work to find the solution.
The integral calculator is able to calculate online the integral of any usual function : Sin (x) + cos (x) = sqrt (2) sin (x + pi/4) so, the integral can be written as: 2s = ∫ π 2 0 ln(sinx)dx + ln(cosx)dx. I’m going to give two methods to evaluate the first one is based on the identity (problem 1), which is an interesting and important result by itself, and the second method is based on the identity.
X and the second function is x.
The integral of x ln x is of the form. I = integral of log [sin (x)]dx from 0 to pi/2. \\int_0^{\\frac {\\pi} {2}}ln(sin(x)).dx my first attempt was to do the following: If we start with the integral $$\int \sin(\ln(x)) dx$$ we can use the substitution $u=\ln(x)$ which gives $du = (1/x)dx$ and $dx = xdu = e^{u} du$.
The integral of sin (lnx) is of the form.
Here are some examples illustrating how to ask for an integral. S = − ∫ 0 π 2 ln(sin( π 2 − t))dt = ∫ π 2 0 ln(cost)dt. Integral of (ln (sin (x))^2. I = ∫ x ln.
A specialty in mathematical expressions is that the multiplication sign can be left out sometimes, for example we write 5x instead of 5*x.
And as the integral is linear: This has to do with the chain rule. Hi, thanks for every one who responded. Pi/4 ln (2) + integral of log [sin (x)]dx from 0 to pi/2.
