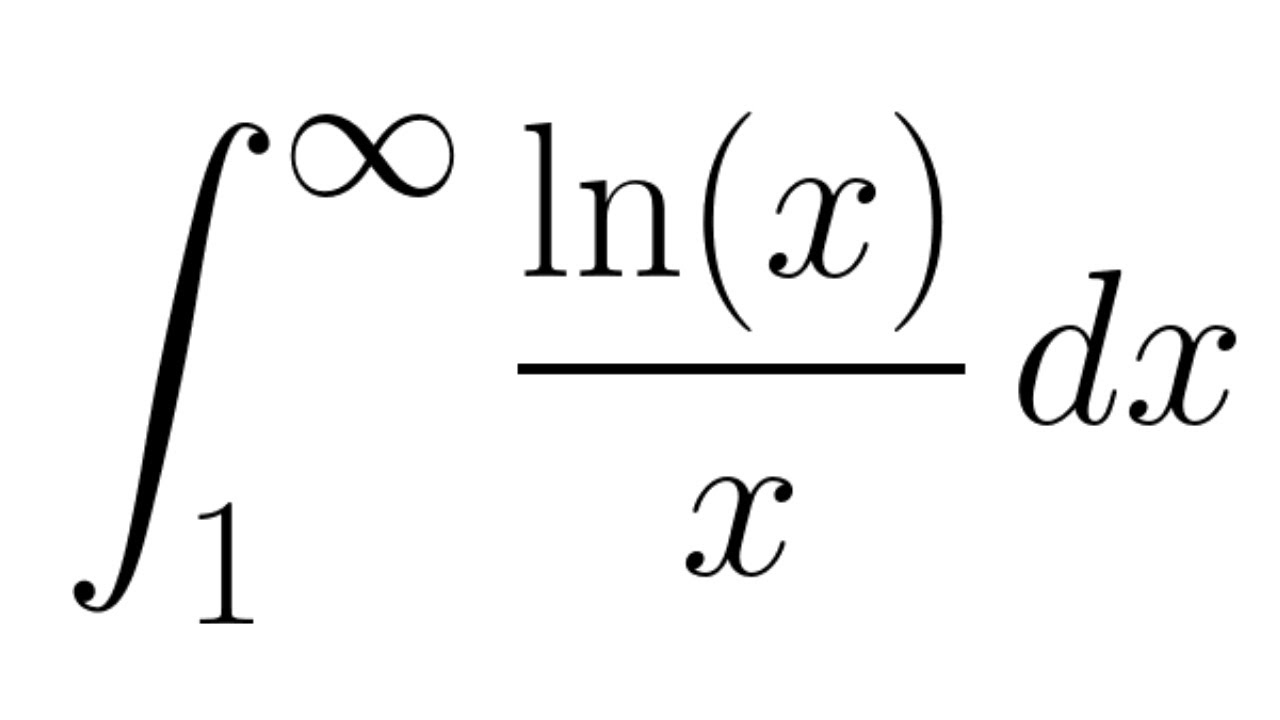The integral (or antiderivative) of 1/x should be a function whose derivative is 1/x. ∫ du 1 + u2. U = tanθ → du = sec2θd(θ) ∫ du 1 + u2 = ∫ sec2θd(θ) 1 +tan2θ.
Integral of 1/(1x)^2 YouTube
D/dx[e ln(x)] = d/dx[x] = 1.
Students, teachers, parents, and everyone can find solutions to their math problems instantly.
The natural number e is found with the definition of ln, the integral of 1/x. D/dx[e ln(x)] = e ln(x) * d/dx[ln(x)] the two are equal, so: ∑ i = 1 n f ( x i ∗) δ x. Partition the interval by.we now have as is positive and decreasing, it takes it's supremum at the left most point of each interval and it's infimum at it's right most point of each interval, for each.
So we have proved the constant on the left.
But we can use the chain rule here: Here ln stands for natural logarithm and 'c' is the integration constant. There is no such thing as the integral of $1/x$. G'(x) = 1 / f'(g(x))
Multiple formulas for the integral of sec x are listed below:
If we choose m = n+1, we get the power we want: The antiderivative of 1/x is ln(|x|). Y=ln (x) d/dx ln (x)= dy/dx. Please subscribe if you liked the video.
In differential calculus we learned that the derivative of ln(x) is 1/x.
Let c o s − 1 x = t, then, x = cos t. We can now evaluate the integral under this change of variables, z 1 0 x p 1 x2 dx= 1 2 z 0 1 p udu= 1 2 2 3 u3 2 u=0 u=1 = 1 3: ∫ du 1 + u2 = tan−1u +c → where u is a function of x. X * d/dx[ln(x)] = 1.
In general, if g(x) is the inverse of f(x):
Instead of changing the bounds of integration, we can rst nd the inde nite integral, z x p 1 x2 dx= 1 2 (1 x2)32; At that point log x is basically a simple straight line passing through a zero y=0 with gradient 1 or some finite value or whatever. Answer to false proof 1 = 0 using integration by parts. The solution is quite simple:
Where c is the integration constant.
But the more popular formula is, ∫ sec x dx = ln |sec x + tan x| + c. However c only has to be constant as a function of x, not n. We don't have to pick the same c for each. The divergence of said integral 1/ln x arises only very close to x=1.
If we divide both sides by n+1 (which is a constant and thus does not influence the derivative), we’ll get the function.
Integration goes the other way: We can cancel out the function, and then we get c = 1 + c. Suppose is positive and decreasing on.then converges if and only if converges. You might know the integral of 1/(x^2+1) but this video shows how we obtain it, using complex numbers.
We are looking for a function f (x) such that f’ (x) = x^n.
We have, i = ∫ c o s − 1 x dx. We can factor the 1 b−a 1 b − a out of the limit as we’ve done and now the limit of the sum should look familiar as that is the definition of the definite integral. The integral of multiplicative inverse of a variable equals to sum of natural logarithm of variable and constant of integration is called the reciprocal rule of integration. ∫ sec2θd(θ) 1 +tan2θ = ∫ (1 + tan2θ)d(θ) 1 +tan2θ.
However, if x is negative then ln(x) is undefined!
As you make n approach 0 from above, you'll get sqrt(x), cbrt(x) etc. E ln(x) * d/dx[ln(x)] = 1. Free math lessons and math homework help from basic math to algebra, geometry and beyond. The indefinite integral on the left equals a function plus a constant c, and the one on the right equals the same function plus a different constant c.
That is not a proof at all.
∫ 1 x d x = ln. Let.by properties of the riemann integral, exists. The mistake in the proof is forgetting the constant of integration. ∴ i = ∫ c o s − 1 x dx.
So, putting in definite integral we get the formula that we were after.
1 b − a ∑ i = 1 n f ( x i ∗) δ x = 1 b − a lim n → ∞. As we just saw, this is ln(x). F'(g(x)) * g'(x) = 1. There is no proof, it's a definition to start with.
You can actually prove d/dx[ln(x)] = 1/x fairly easy:
The only thing that needs to be proven is.