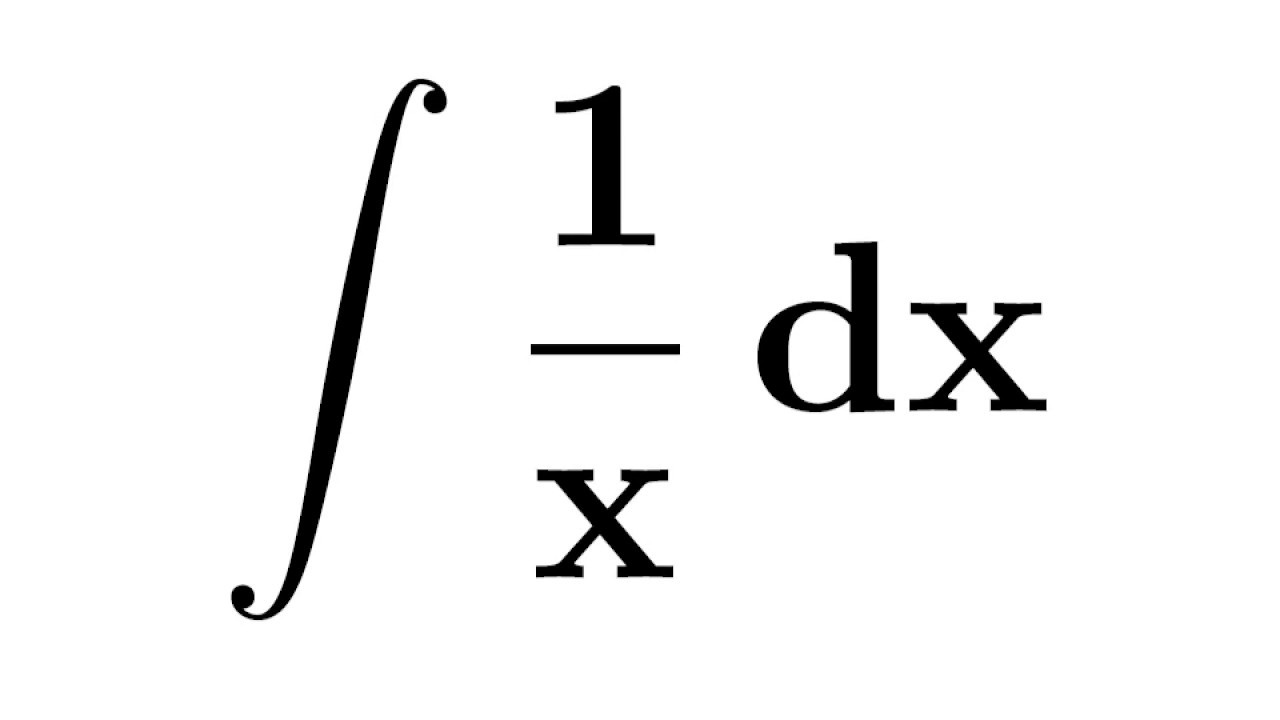∫ e tan x ( sec x −. Find d u d x d u d x. 0.1 mole of a carbohydrate with empirical formula ch 2 o contains 1g of hydrogen.
Integral of 1/(1+x) YouTube
Find the integral 1/ (x+1) 1 x + 1 1 x + 1.
Roughly speaking, an integral is a sum over an infinity of zeros, expressed as the limit of the sum of values of the function times small intervals, as the intervals go to zero in size.
By the fundamental theorem of calculus, we get: On an interval that excludes 0, the antiderivative of 1 x is. The integral of one over sqrt (x^2+1) dx. My notebook, the symbolab way.
What is its molecular formula?
The integral calculator supports definite and indefinite integrals (antiderivatives) as well as integrating functions with many variables. The integral (or antiderivative) of 1/x should be a function whose derivative is 1/x. ∫ [xe x / (1 + x) 2] dx. Feb 9, 2022 @ 19:54.
If ∫ sin 2 0 1 0 x sec 2 x − 2 0 1 0 d x = ( sin x) 2 0 1 0 p ( x) + c , where c is arbitrary constant then value of p ( 3 π ) hard.
As we just saw, this is ln (x). ∫ [x / 1 + x] dx = ∫ [x (1 / x)/ 1(1 / x) + x(1 / x)] dx. Interactive graphs/plots help visualize and better understand the functions. In differential calculus we learned that the derivative of ln (x) is 1/x.
Integration is the process of reverse differentiation, that is.
(2) [ex / (x + 1)] + c. Hi aya, ∫ (1/dx) is a combination of symbols that has no mathematical meaning. Below is the integrand and the two solutions, with c = π /2 in the second case. Derivatives derivative applications limits integrals integral applications integral approximation series ode multivariable calculus laplace transform taylor/maclaurin series fourier series.
∫ [1 / (1/x) + (1)] dx.
= [e x / (x + 1)] + c. Not sure where to go from here. The integral of arctan can be calculated using the integration by parts method. Let u = x+1 u = x + 1.
Integral of 1/ (x^2) \square!
Lnx = ∫ x 1 1 t dt for x > 0. Therefore to make it represent the form ∫ f'(x)/f(x) dx do: You can also check your answers! D dx (lnx) = 1 x for x > 0.
For more about how to use the integral calculator, go to help or take a look at the examples.
Let u = x + 1 u = x + 1. Cos 2 x dx = 0 4 plus 0 44 plus 0 444 to 2n terms equal: Integrate 1/(cos(x)+2) from 0 to 2pi; Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;
Here are some examples illustrating how to ask for an integral.
Rewrite using u u and d d u u. From that and the chain rule, we also get d dx (ln( − x)) = 1 x for x < 0. However, if x is negative then ln (x) is undefined! To avoid ambiguous queries, make sure to use parentheses where necessary.
Table of basic integrals basic forms (1) z xndx= 1 n+ 1 xn+1;
Then du = dx d u = d x. N6= 1 (2) z 1 x dx= lnjxj (3) z udv= uv z vdu (4) z 1 ax+ b dx= 1 a lnjax+ bj integrals of rational functions (5) z 1 (x+ a)2 dx= 1 x+ a (6) z (x+ a)ndx= (x+ a)n+1 n+ 1;n6= 1 (7) z x(x+ a)ndx= (x+ a)n+1((n+ 1)x a) (n+ 1)(n+ 2) (8) z 1 1 + x2 dx= tan 1 x (9) z 1 a2 + x2 dx= 1 a tan 1. Lnx if the interval consists of positive numbers and it is ln( − x) if the interval consists of negative numbers. A valid expression would be ∫ (1/x)dx for example.
0.4i+0.8j+ck represents a unit vector when c is
I mean, when we take an integral and want it to be meaningful, we usually take definite integral, not indefinite integral. For $1/x$, the definite integral cannot be taken over an interval that contains 0, the two boundaries should be both positive or negative. So $\int_a^b \frac{1}{x}dx=\log(b/a)$, no mistake will be made.