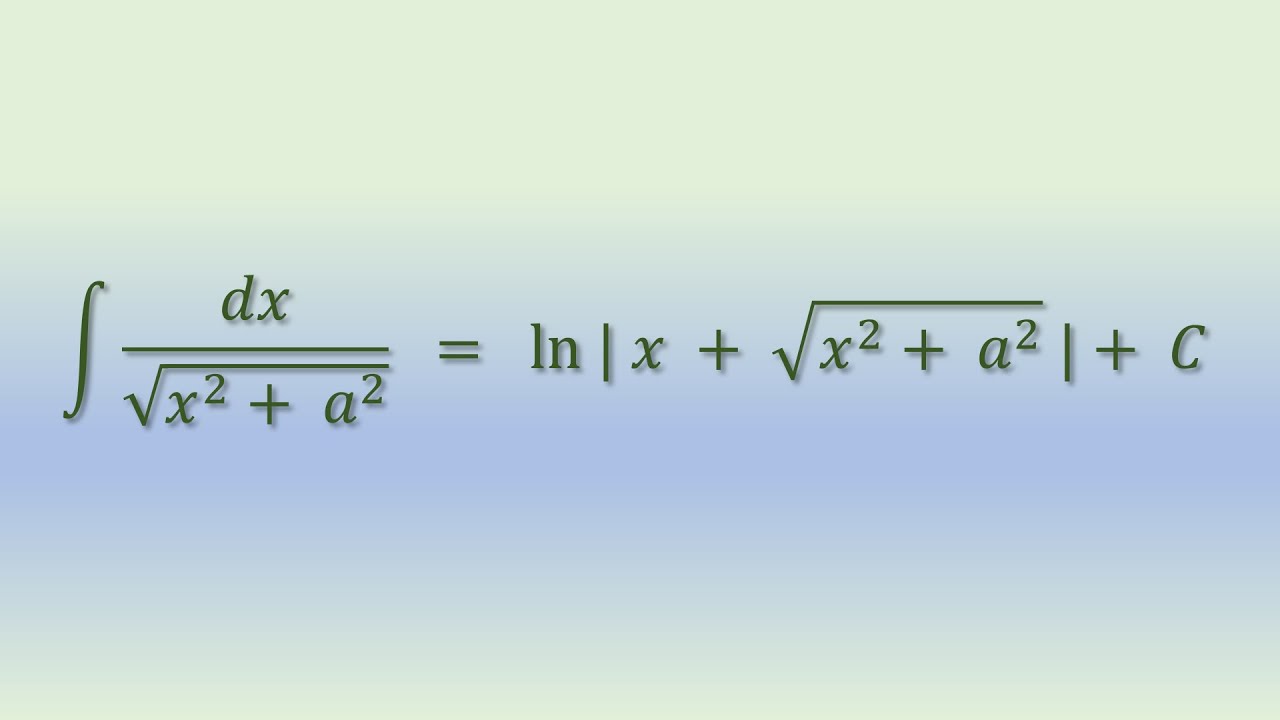Your first 5 questions are on us! Note that tan2θ = sec2θ − 1: Sometimes an approximation to a definite integral is desired.
Integration of 1/sqrt(a^2+x^2)dx Shortcut YouTube
The process of solving for antiderivatives is antidifferentiation (or indefinite integration).
Through the pythagorean theorem we see that the opposite side is √x2 − a2.
I will have to look more into this. N6= 1 (2) z 1 x dx= lnjxj (3) z udv= uv z vdu (4) z 1 ax+ b dx= 1 a lnjax+ bj integrals of rational functions (5) z 1 (x+ a)2 dx= 1 x+ a (6) z (x+ a)ndx= (x+ a)n+1 n+ 1;n6= 1 (7) z x(x+ a)ndx= (x+ a)n+1((n+ 1)x a) (n+ 1)(n+ 2) (8) z 1 1 + x2 dx= tan 1 x (9) z 1 a2 + x2 dx= 1 a tan 1. Thus we have a right triangle where x is the hypotenuse and a is the adjacent side. Example 9 (ii) important → chapter 7 class 12 integrals (term 2) serial order wise;
Well, my way of approaching this integral would be, so, now the above integral can be solved by using integral by parts, try doing it!
( x) d x = ( − c o s ( π)) − ( − c o s ( 0)) = 2. A common way to do so is to place thin rectangles under the curve and add the signed areas together. Asked mar 29, 2018 in class xii maths by nikita74 expert (11.2k points) integrate∫√1+x 2 /x 4 dx. This integral can be written as.
This means ∫π 0 sin(x)dx= (−cos(π))−(−cos(0)) =2 ∫ 0 π sin.
Indefinite integrals of form sqrt (x. 20, 2021 by teachoo next: The attempt at a solution. From x = asecθ we see that secθ = x a.
) in calculus, an antiderivative, primitive, or indefinite integral of a function f is a function f whose derivative is equal to f, i.e., f ′ = f.
Stack exchange network stack exchange network consists of 179 q&a communities including stack overflow , the largest, most trusted online community for developers to learn. Here we have another way to see this: 1st) right y or if it it is in differentiation then dy/dx in a simpler form : Let x = sec u:
Table of basic integrals basic forms (1) z xndx= 1 n+ 1 xn+1;
= ∫ tan^2 (u) du. Antiderivatives are related to definite integrals through the fundamental theorem of calculus: We will use the substitution x = asecθ. $$ finally we can use:
= ∫ tan u tan u du.
Find the area of the surface generated when the given curve is revolved about the given axis. Ok, so after an integration by parts, now you have to integrate x^2/sqrt (x^2+1). Using the formula above, equation (i) becomes.