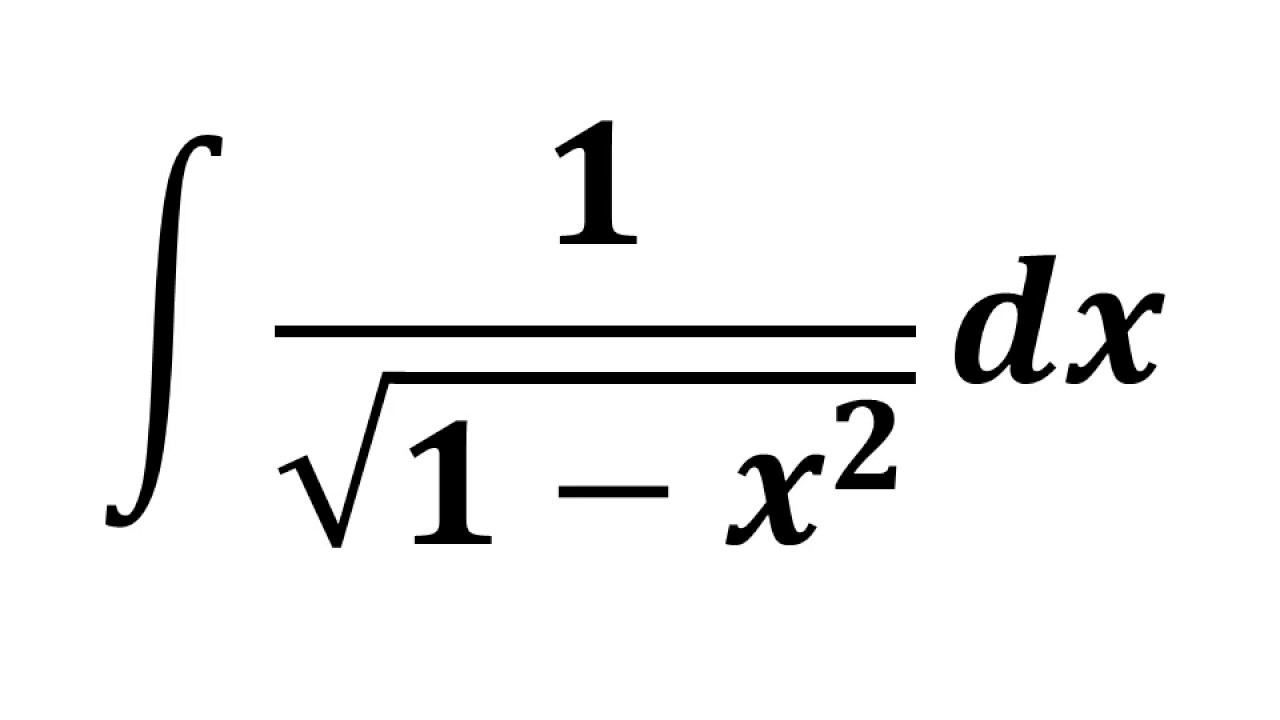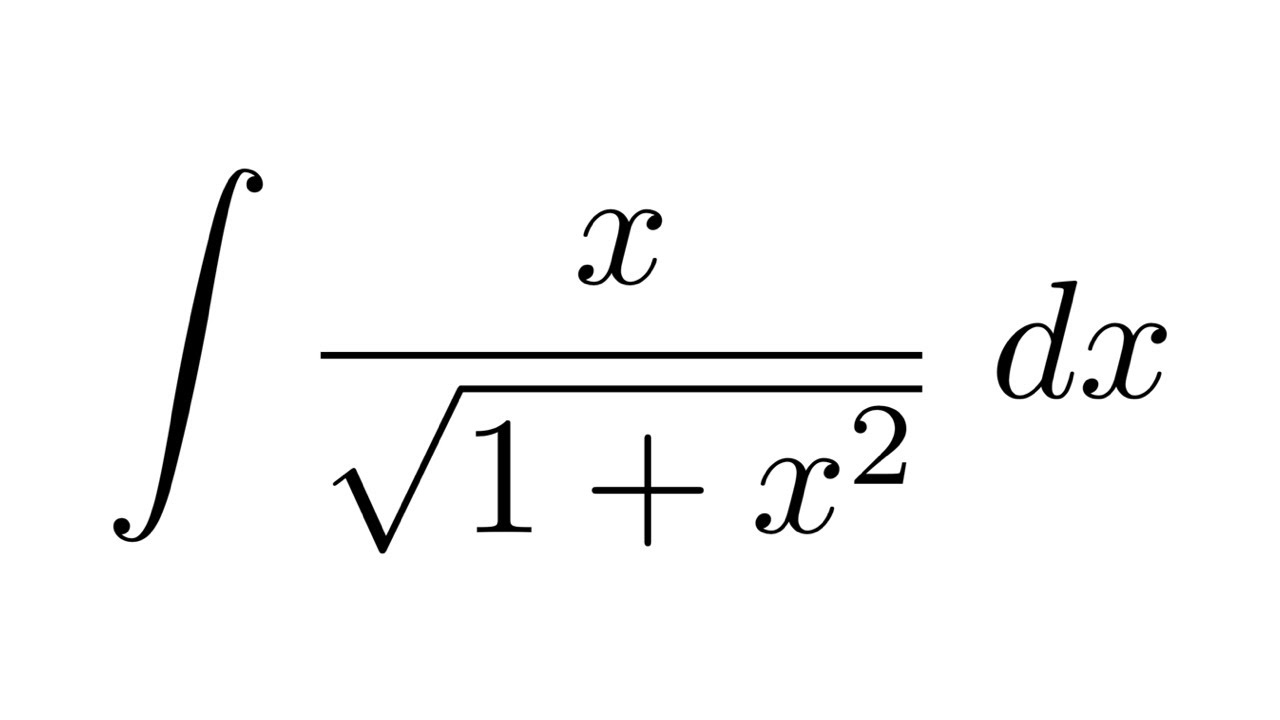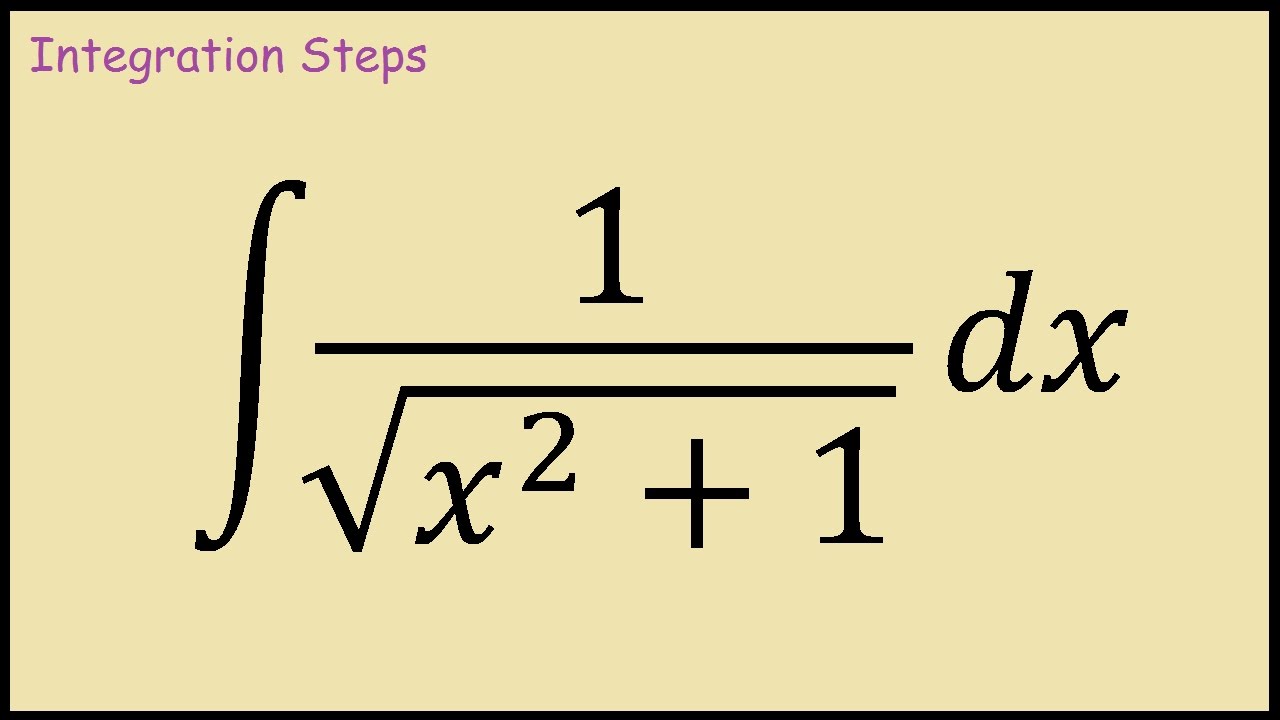= ∫ tan u tan u du. Let x = sec u: As an antiderivative we may know the derivative of arcsine.
Integral of sqrt(1+x^2)/x (substitution + partial fraction
= ∫ tan^2 (u) du.
∫ 1 1 − x 2 d x = sin − 1.
We can start with this may be rewritten as us now we take let us differentiate this. Interactive graphs/plots help visualize and better understand the functions. We can solve the integral \int\frac{1}{\sqrt{\left(a^2+x^2\right)^{3}}}dx by applying integration method of trigonometric substitution using the substitution. The objective is to evaluate the given integral.
Let $ x = \sinh \theta$, then set $$i=\int \sqrt{1+x^2}dx$$ whence \begin{align} i &= \int \sqrt{1+x^2}dx \\ &= \int \sqrt{1+\sinh^2 \theta}\cosh \theta d \theta \\ &= \int \cosh^2 \theta d \theta \\ &= \frac{1}{2}\int 1 + \cosh 2 \theta d \theta \\ &= \frac{1}{2}\theta+\frac{1}{4}\sinh 2 \theta + c\\ &= \frac{1}{2}\sinh^{.
We can now calculate dx with respect to this new substitution as well. Thus after substitution, our integral becomes cos (u)/cos (u)du = the integral of 1 du = u + k where k is the constant of integration. Now, in order to rewrite d\theta in terms of dx, we need to find the derivative of x. The integral of sin(x)cos(x)dx next page :
Let us investigate this from a nonstandard viewpoint.
The attempt at a solution. Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi; For more about how to use the integral calculator, go to help or take a look at the examples. The indefinite integral of one by square root of one minus square of a variable is equal to the sum of the inverse.
Here, take u =1+x2 u.
Since x = sin (u), dx/du = cos (u) and so dx = cos (u)du. Let i=[a,b] be a closed and bounded interval of real numbers, where a and b are real numbers with b>a, and let \nu be an infinite hyperinteger. Integrate functions using the trigonometric substitution method step by step. The definite integral of from to , denoted , is defined to be the signed area between and the axis, from to.
Learn how to solve integrals of rational functions problems step by step online.
To prove this formula, consider. That is, if we choose a value for ##c_1##, what is the corresponding choice for ##c_2##? Now, in order to rewrite d\theta in terms of dx, we need to find the derivative of x. Example 1 (i) example 1 (ii) example 1 (iii) example 2 (i).
The integral calculator supports definite and indefinite integrals (antiderivatives) as well as integrating functions with many variables.
The integral of 1 over the square root of 1 − x 2 is of the form. Both types of integrals are tied together by the fundamental theorem of calculus. Type in any integral to get the solution, steps and graph You can also check your answers!