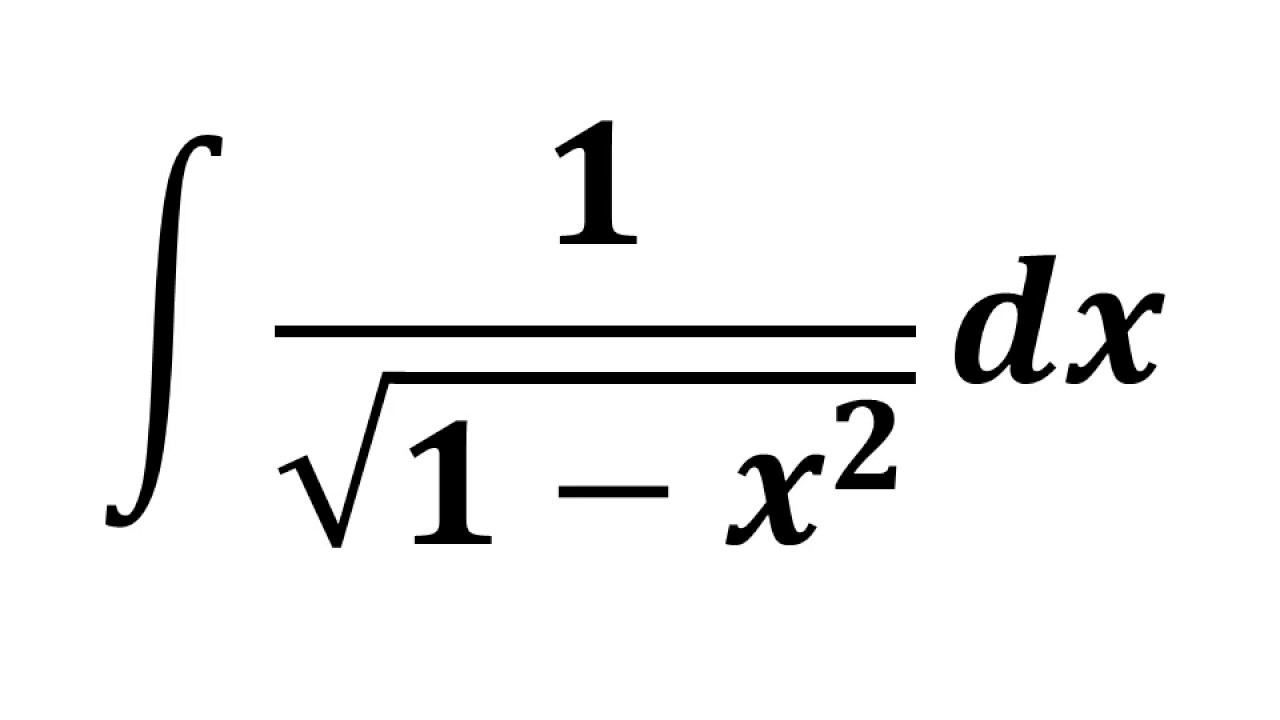To prove this formula, putting x = a sec. Rewrite using u u and d d u u. Tanθ = √sec2θ −1 = √ x2 a2 − 1.
INTEGRAL OF SQARE ROOT OF (x^2a^2) integral of 1
Integrate 1/(cos(x)+2) from 0 to 2pi;
Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;
I = ∫secθdθ = ln|secθ + tanθ|. Our trigonometry then gets us. This implies that dx = sec2θdθ. I = ∫ 1 √1 +x2 dx.
We think that the integrand of i has the other factor 1 and integrate partially:
The integration is of the form. To prove this formula, putting x = a cosh. Perhaps the simplest is to write: I = ln∣∣x +√1 + x2∣∣ +c.
We can rewrite in several ways.
T we have d x = a sinh. Now that we have integrated the secant, note that due to the first substitution, secθ = x a. I = ∫ 1 √1 + tan2θ sec2θdθ. In calculus, an antiderivative, primitive, or indefinite integral of a function f is a function f whose derivative is equal to f, i.e., f ′ = f.
Note that tanθ = x and secθ = √1 +tan2θ = √1 +x2:
Here are some examples illustrating how to ask for an integral. To avoid ambiguous queries, make sure to use parentheses where necessary. Joy chiangintegral of sec^3x here: That was the whole point of the substitution, it is a rationalizing substitution that makes the square root simple.
Ln(secθ +tanθ) + c = ln( x a + √x2 a2 − 1) + c.
Find d u d x d u d x. This integral can be written as. So the given integral takes the form.