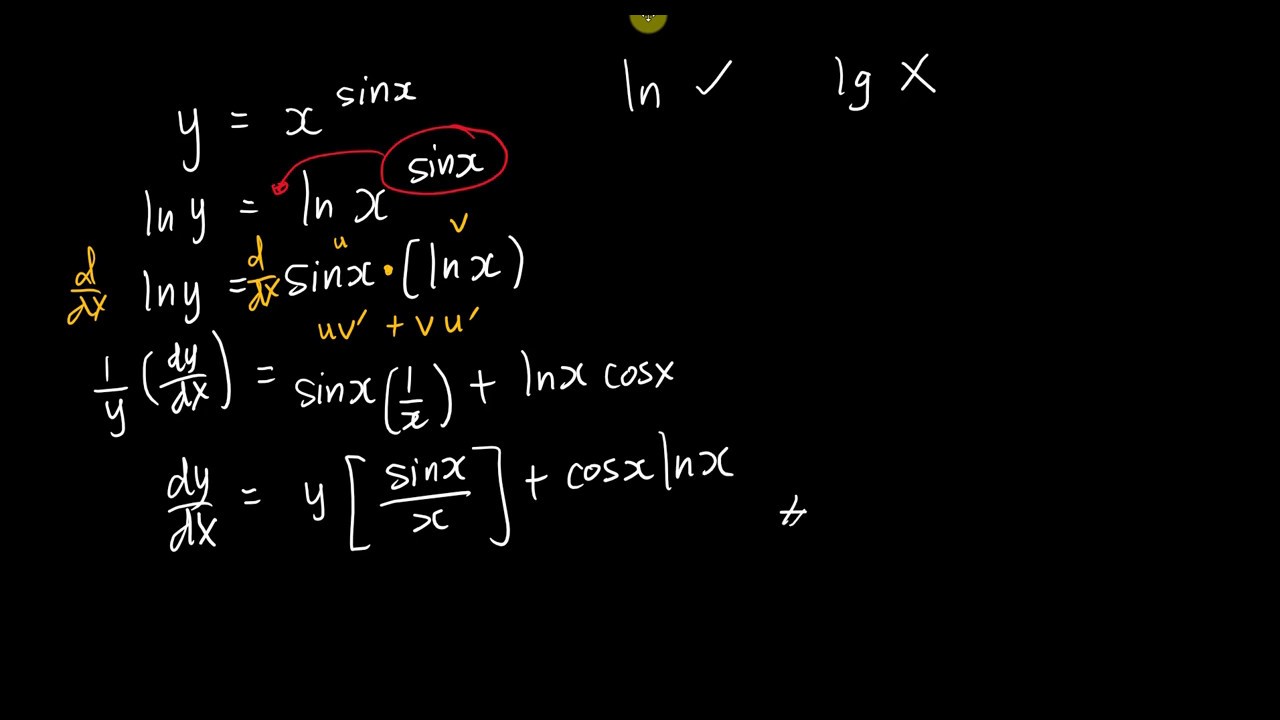As derived above, integration by parts uv formula is: Propiedades y formas básicas de las integrales, integrales trigonométricas, integrales trigonométricas inversas. Z udv = uv − z v du.
ひどい Uv Formula サムコハメ
Uv differentiation formula helps to find the differentiation of the product of two functions.
The product rule is one of the derivative rules that we use to find the derivative of two or more functions.
A s2 1 area of a triangle: The trigonometric functions are simplified into integrable functions and then their integrals are evaluated. ∫ sec x (tan x) dx = sec x + c. ∫ cosx.dx = sinx + c;
* see if u and v are both different functions in x then no such direct formula is there for integration of (u/v) dx.
The list of basic integral formulas are. What are the integration formulas for trigonometric functions? Frequently, we choose u so that the derivative of u is simpler than u. We again apply integration by parts (with u = sin x and dv = e x dx this time).
X sin (x) − ∫ sin (x) dx.
2 1 sin ( ) 1 cos(2 )x 2 sin tan cos x x x 1 sec cos x x cos( ) cos( ) x x 22sin ( ) cos ( ) 1xx 2 1 cos ( ) 1 cos(2 )x 2 cos cot sin x x x 1 csc sin x x sin( ) sin( ) x x 22tan ( ) 1 sec ( )x x geometry fomulas: X sin (x) + cos (x) + c. ∫ a dx = ax+ c. The integration formula of uv :
The uv formula of integral is generally used to calculate the integration by parts.
Integration by parts uv formula. ∫ sec 2 x dx = tan x + c. ∫ b a udv = uv|b a −∫ b a vdu ∫ a b u d v = u v | a b − ∫ a b v d u. This method of integration is often used for integrating products of two functions.
∫x cox x dx = x sinx + cos x + c.
∫ cos x dx = sin x + c. Integration by parts, definite integrals. Integrals of some special function s. V = cos (x) so now it is in the format ∫u v dx we can proceed:
∫ v dx = ∫ cos (x) dx = sin (x) (see integration rules) now we can put it together:
To apply this formula we must choose dv so that we can integrate it! ∫ 1 dx = x + c. Let u and v are two functions then the formula of integration is. This can be expressed as:
Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − integrals of rational and irrational functions 1 1 n x dx cn x n + = + ∫ + 1 dx x cln x ∫ = + ∫cdx cx c= + 2 2 x ∫xdx c= + 3 2 3 x ∫x dx c= +
You just try to make numerator as a differential coefficient of denominator and then substitute as denominator =t and. Uv integration is one of the important methods to solve the integration problems. Let us assume here log x is the first function and constant 1 is the second function. To find the integration of the given expression we use the integration by parts formula:
Note that the uv|b a u v | a b in the first term is just the standard integral evaluation notation that you should be familiar with at this point.
∫ sec 2 x.dx =. ∫u v dx = u∫v dx − ∫u’ (∫v dx) dx ∫ x n dx = ( (x n+1 )/ (n+1))+c ; The basic integration formulas for trigonometric functions are as follows.
Strategy for using integration by parts recall the integration by parts formula:
U' = x' = 1. Then the integral of the second function is x.