Z sin(2x)cos(5x) dx here, we use the sum formulas: By repeated use of the reduction formulas we can integrate any even power of tan x or cot x. Cos((a b)x) a b +c the other integrals of products of sine and cosine follow similarly.
PPT Inverse Trig Functions and Standard Integrals
The list of basic integral formulas are.
We can also work the integral of any odd power of tan x or cot x down to an expression involving ∫ tan x or ∫ cot x.
Integrals involving sin(x) and cos(x): In this video, i discussed how to find the integration of two trigonometric functions. Some of the following trigonometry identities may be needed. In a simple straight language integration can be defined as the measure, which basically assigns numbers to the several functions.the numbers are basically assigned which may describe the displacement,volume or area etc of such concerned function.
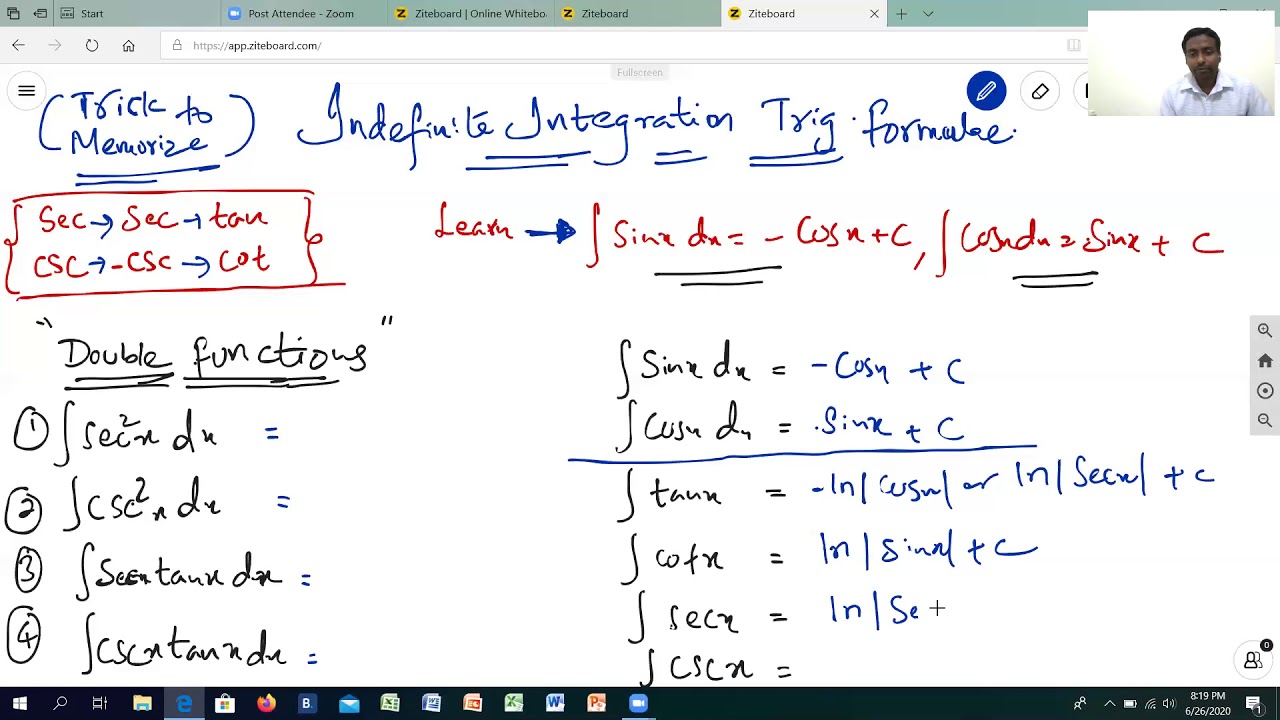
∫ cos x dx = sin x + c.
X d x = sin. ∫ a dx = ax+ c. Definite integrals of trig functions. Generally, if the function is any trigonometric function, and is its derivative, in all formulas the constant a is.
∫ 1 dx = x + c.
However, only three integration formulas are noted in the rule on integration formulas resulting in inverse trigonometric functions because the remaining three are negative versions of the ones we use. ∫cot x dx = ln|sin x| + c. The list of integral rules of trigonometric functions with proofs. ∫cos x dx = sin x + c.
∫sec2x dx = tan x + c.
Integrals involving sec(x) and tan(x): Integrals of trigonometric functions ∫sin cosxdx x c= − + ∫cos sinxdx x c= + ∫tan ln secxdx x c= + ∫sec ln tan secxdx x x c= + + sin sin cos2 1( ) 2 ∫ xdx x x x c= − + cos sin cos2 1 ( ) 2 ∫ xdx x x x c= + + ∫tan tan2 xdx x x c= − + ∫sec tan2 xdx x c= + integrals of exponential and logarithmic functions ∫ln lnxdx x x x c= − + ( ) 1 1 2 ln ln 1 1 n n x xdx x cn x x n n Cos(ax)cos(bx)dx = 1 2 sin((a b)x) a b + sin((a+b)x) a+b +c. Integrals that produce inverse trigonometric functions.
1 2 sin((a+b)x)+sin((a b)x) dx = 1 2.
Depending upon your instructor, you may be expected to memorize these antiderivatives. In integration we basically take the infinitesimal data as the combination. U) + c = − ln. If a 6= b, then:
3 + p 2;cos2 ax (69) z cos3 axdx= 3sinax 4a + sin3ax 12a (70) z cosaxsinbxdx=.
Sin( )cos( ) = 1 2 (sin( + ) + sin( )) doing a similar thing to the cos formula, one gets rules that will help for integrals of the form cos( )cos( ) and sin( )sin( ). ∫ du √a2−u2 =sin−1(u a)+c ∫ d u a 2 − u 2 = sin − 1 ( u a) + c. ∫tan x dx = ln|sec x| + c. A.) b.) e.) it is assumed that you are familiar with the following rules of differentiation.
For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions.
The six basic formulas for integration involving trigonometric functions are stated in terms of appropriate pairs of. ∫sec x dx = ln|tan x + sec x| + c. ∫ du a2+u2 = 1 a tan−1(u a)+c ∫ d u a 2 + u 2 = 1 a tan − 1 ( u a) + c. Dv exponential functions (e33xx,5 ,etc) functions that appear at the top of the list are more like to be u, functions at the bottom of the list are more like to be dv.
The list of fundamental integral rules of trigonometric functions with proofs.
There are six inverse trigonometric functions. Adding the two, one gets: Current location > math formulas > trigonometry > integrals of trigonometric functions. In the following formulas all letters are positive.
The indefinite integral of \ (f\left ( x \right)\) is thus represented as \ (\int f \left ( x.
The only difference is whether the integrand is positive or negative. Fundamental integration formulas of trigonometric functions. ∫ du u√u2−a2 = 1 a sec−1(u a)+c ∫ d u u u 2 − a 2 = 1 a sec − 1 ( u a) + c. In the video, we work out the antiderivatives of the four remaining trig functions.
3 2;cos2 ax (65) z sin3 axdx= 3cosax 4a + cos3ax 12a (66) z cosaxdx= 1 a sinax (67) z cos2 axdx= x 2 + sin2ax 4a (68) z cosp axdx= 1 a(1 + p) cos1+p ax 2f 1 1 + p 2;
X d x = − cos. Integration of trigonometric functions formulas. 0 formulas included in custom cheat sheet. ∫ sec x (tan x) dx = sec x + c.
The reduction formulas for the other trigonometric functions are obtained by using integration by parts.
For a complete list of antiderivative functions, see lists of integrals. ∫ x n dx = ( (x n+1 )/ (n+1))+c ; Sin(ax)sin(bx)dx = 1 2 sin((a b)x) a b. The antiderivatives of tangent and cotangent are easy to compute, but not so much secant and cosecant.
X d x = sin.
Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; The following are some standard trigonometric integration formulas with proofs. 11 rows current location > math formulas > calculus > integrals of trigonometric functions.