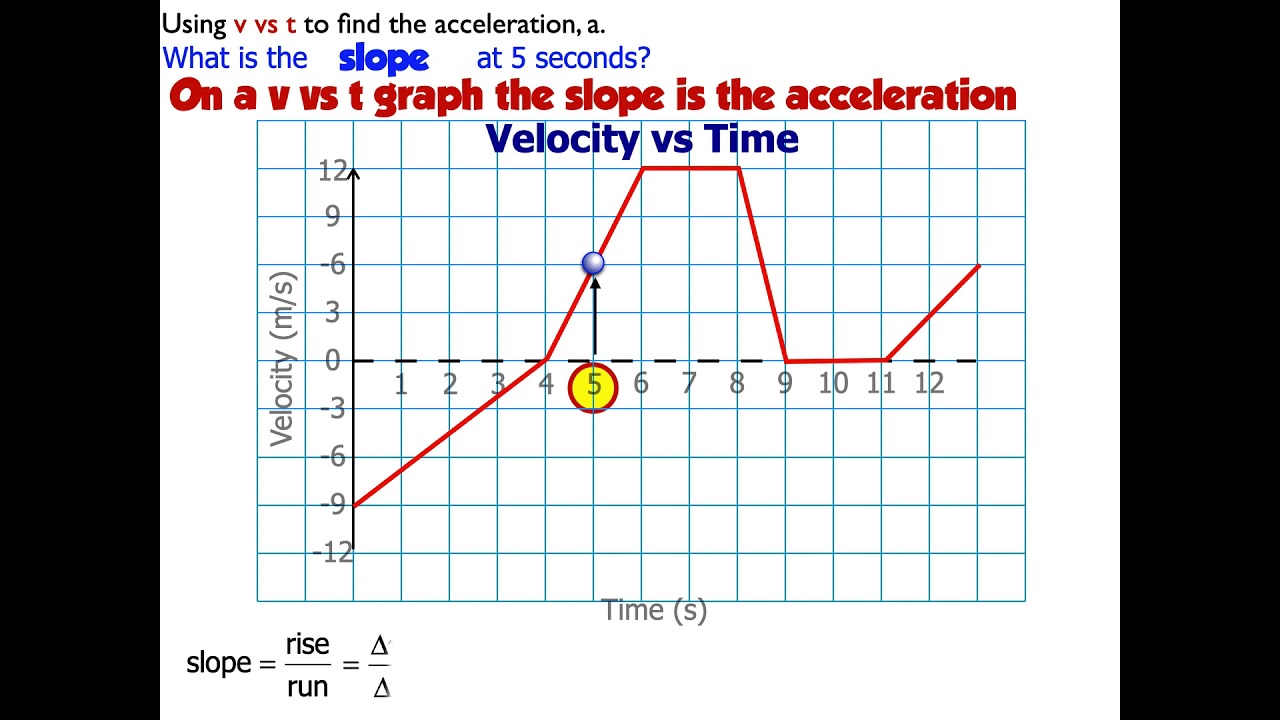
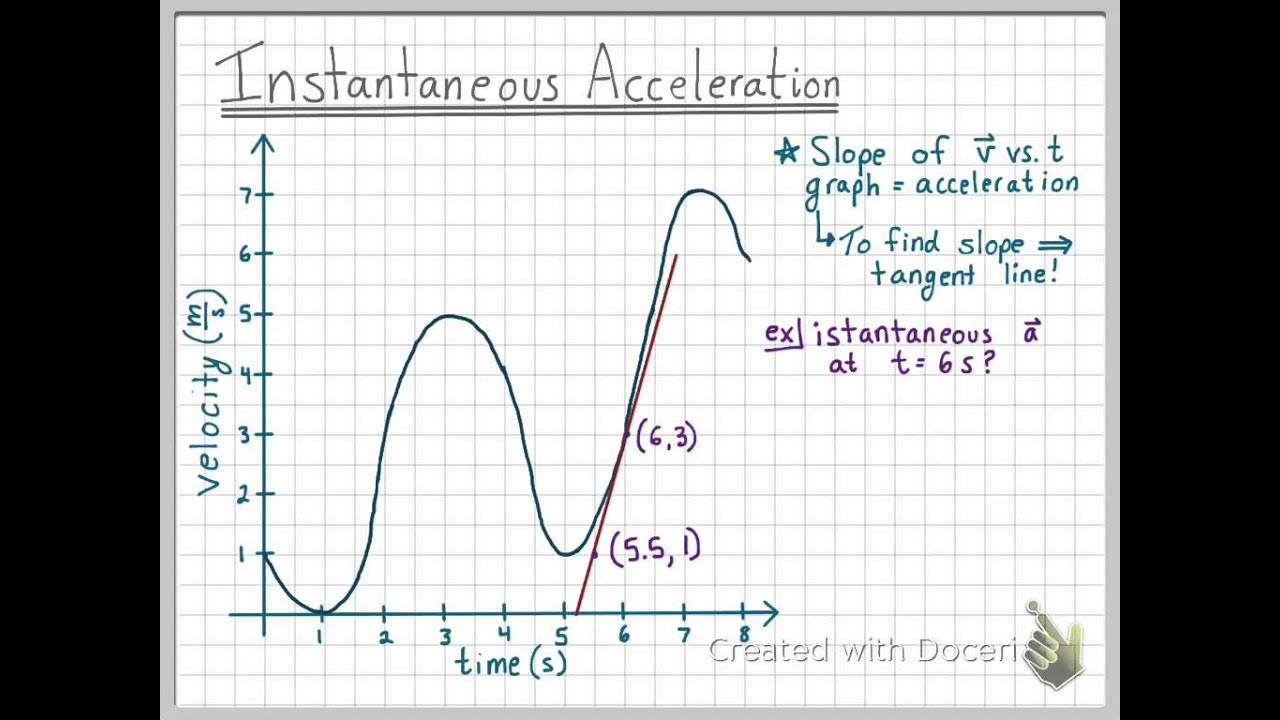
The acceleration is given by finding the slope of the velocity graph. The horizontal instantaneous velocity is: Figure 3.14 in a graph of velocity versus time, instantaneous acceleration is the slope of the tangent line.
Solved 1) What Is The Instantaneous Velocity At Point ? M
Velocity graphing speed the steepness of a line on a graph is called slope.
In fact, if you represent an object's displacement with a line on a graph, the slope of the line at any given point is equal to the object's instantaneous velocity at that point.
Instantaneous velocity formula is used to determine the rate of change of displacement of the given body at any specific instant of time. “the limit of the average velocity as elapsed time reaches zero, or the derivative of displacement x with respect to time t, is the instantaneous velocity of an object.” To find the average velocity, recall that v avg = δ d δ t = d f − d 0 t f − t 0 v avg = δ d δ t = d f − d 0 t f − t 0 Follow this answer to receive notifications.
Average speed is total distance traveled divided by elapsed time.
In the above figure graph of position versus time, the instantaneous velocity is the slope of the tangent line at a given point. Calculus, developed by sir isaac newton and leibniz, can calculate small changes over time by. Intro to vectors and scalars. Finally, the instantaneous velocity will be displayed in the output field
The horizontal velocity of the ball is a constant value of 6.0 m/s in the +x direction.
Finding the instantaneous velocity from a velocity vs time graph. Whenever an object has a constant velocity, the average velocity will be the same as the instantaneous velocity. Finding the instantaneous velocity from a velocity vs time graph. If an object has equal displacements in equal intervals of time, it is said to possess uniform.
In the limiting stage, the chord r s would become the tangent to the curve.
In terms of the graph, instantaneous velocity at a moment, is the slope of the tangent line drawn at a point on the curve, corresponding to that particular instant. Instantaneous speed is found by taking the absolute value of instantaneous velocity, and it is always positive. When δ t approaches the zero the point r approaches point s. Now click the button “calculate x” to get the result step 3:
To calculate the average velocity between two points and , we divide the change of position by the change in time.
(b) the instantaneous velocity v is the limit of the average velocity as h approaches 0. Instantaneous velocity and instantaneous speed from graphs (practice) | khan academy. Enter the displacement, time, x for the unknown in the respective input field step 2: Instantaneous velocity is the limiting value of the average velocity δ x δ y as δ y approaches zero.
The average velocity is the change in height divided by the change in time.
At t = 3 ≈ 17.7 − 5.1 4 − 2 = 12.6 2 = 6.3. Hi everybody here iam discussed about instantaneous speed and velocity in detail. Here iam also discussed about displacement time graph velocity time graph. To graph an object's displacement, use the x axis to represent time and the.
So, we will estimate the instantaneous velocity with the average velocity over [ 2, 4] (the average velocity over [ 2, 4] is the slope of the line connecting the points [ 2, 5.1] and [ 4, 17.7] ).
The instantaneous velocity can just be read off of the graph. At {eq}t = a {/eq}, sketch a. At the lower right in red is the the equation v = delta x/delta t. Instantaneous velocity is a vector and can be negative.
So we have, v → = lim δ t → 0 δ x → δ y = d x → d t.
These can be solved using the scalar multiple rule and the power rule for derivatives: In a graph of position versus time, the instantaneous velocity is the slope of the tangent line at a given point. A particle moves rectilinearly with constant speed then the instantaneous velocity. The instantaneous velocity at any time, t is given by;
The instantaneous velocity at point is equal to the slope of the position graph at point.
\begin{aligned}\vec{v} &= \dfrac{\vec{ds}}{dt}\\\end{aligned} here, \vec{ds} is the displacement of the particle in a small time interval, dt. If an object has unequal displacements in equal intervals. What is the instantaneous velocity of the object at t 4s?