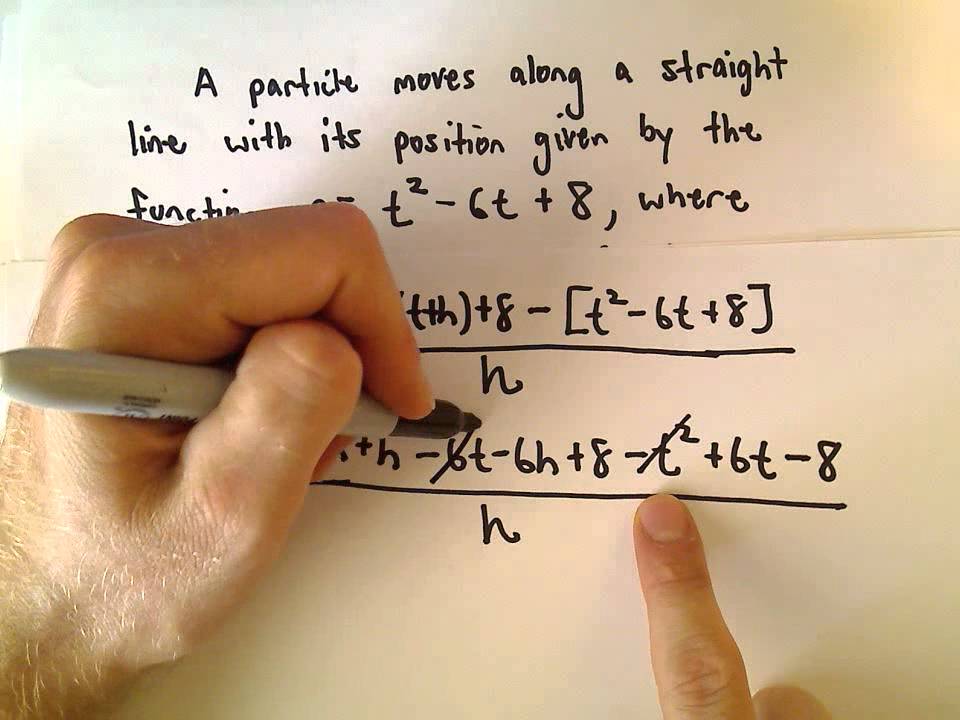Vi= instantaneous velocity of any moving object. Check out this dialogue between two calculus students (based on a true story): Derive the formula of instantaneous acceleration (step by step)
PPT Average Velocity and Instantaneous Velocity
V ( t) = d d t x ( t).
Compute its instantaneous velocity at time t = 5s.
We can now state the defining equation for instantaneous velocity, which is the infinitesimal limit of. The instantaneous acceleration of an object is the limit of the average acceleration as the elapsed time approaches zero, or the derivative of velocity v with respect to t: The instantaneous rate of change is also a limit. Now we can find the slope of the green line.
V(5) = 8(5) + 10.
Devyn hey riley, i’ve been thinking about limits. Instantaneous velocity formula of the given body at any specific instant can be formulated as: \( v_{int} = \lim_{\delta t\to 0} \frac{\delta x}{\delta t} = \frac {dx}{dt} \) wherewith respect to time t, x is the given function. The function is x = 4t 2 + 10t + 6.
Δt = a very small portion of time or time interval.
The instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero, or the derivative of x with respect to t: Instead, we could choose a blue line that’s even closer. The horizontal velocity of the ball is a constant value of 6.0 m/s in the +x direction. When we compute average velocity, we look at to obtain the (instantaneous) velocity, we want the change in time to “go to” zero.
In the following video, we illustrate this concept by considering the instantaneous velocity at time t = 2 of a particle with position s ( t) = 4 t 2 + 3, where t is time in seconds, and s is position in feet.
Thus, ω ( lim δ t → 0) = δ θ δ t = dθ dt if we know θ ( t ), we can find the angular velocity ω by differentiation. To calculate instantaneous velocity, the \(\delta\) t needs to be zero. Average and instantaneous rate of change of a function in the last section, we calculated the average velocity for a position function s(t), which describes the position of an object ( traveling in a straight line) at time t. Thus, v (t) = dx(t)/dt.
But again, it isn’t quite the line we want.
For time t = 5s, the instantaneous velocity is articulated as, v(t) = 8t + 10. The vertical instantaneous velocity is: The instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero, or the derivative of x with respect to t: Lim t → a δ s δ t = lim t → a s ( t) − s ( a) t − a.
Insert the values of t 1 = t and t 2 = t + δt into the equation for the average velocity and take the limit as.
Hold on to your hat, you’ve arrived at one of the big “ah ha!” moments in the development of differential calculus. We use limits to compute instantaneous velocity. Differentiating the provided function with respect to t, we get. Why is the instantaneous rate of change is a limit?
How do you find instantaneous velocity using limits?
Instantaneous velocity limit formula the instantaneous velocity of any object is the limit of the average velocity as the time approaches zero. S = (6t 2 + 2t + 4) velocity (v) = \ ( \frac {ds} {dt} \) = \ ( \frac {d (6t^2 + 2t + 4)} {dt}\) = 12t + 2. Instantaneous velocity formula “instantaneous velocity is total displacement divided by total time as the time interval approaches zero. We saw that the average velocity over the time interval [t 1;t 2] is given by v = s.
Q what does this have to do with velocity?
To avoid these tedious calculations, we would really like to have a formula. Above explained instantaneous velocity equation can be further simplified as follows: Instantaneous speed is defined as the limit of the average speed function as the elapsed time approaches zero. So, if we have to find out the instantaneous velocity at t = 5 sec, then we will put the value of t in the obtained expression of velocity.
Thus for the known function, instantaneous velocity is 50 m/s.
Thanks to all of you who support me on patreon. The instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero, or the derivative of x with respect to t: The horizontal instantaneous velocity is: V y = c(2t) v y = 2ct.
The fact that the elapsed time never gets to zero doesn’t affect the precision of the answer to this limit problem — the answer is exactly 32.
At t = 4.0 s, the vertical instantaneous velocity is: Now the slope of the blue line is 52.25−50 5.5−5 = 2.25 0.5 = 4.5 52.25 − 50 5.5 − 5. Two young mathematicians discuss limits and instantaneous velocity. The (instantaneous) angular velocity ω is the limit of the ratio in equation above as δ t approaches zero.
This can be determined in a simple way by applying formula as follows:
Instantaneous velocity at t = 5 sec = (12×5 + 2) = 62 m/s. It’s 54−50 6−5 = 4 1 = 4 54 − 50 6 − 5 = 4 1 = 4, since that is what rise over run tells us. About press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features press copyright contact us creators. Getting the equation or formula (step by step)