Find the instantaneous velocity at t = 1, 2, 3, and 5 s. Displacement = (6×5 2 + 2×5 + 4) = 164 m. The instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero, or the derivative of x with respect to t:
Instantaneous Acceleration YouTube
Let's consider a particle whose velocity (in meters per second) at an instant t (in seconds) is given by 2 t 2:
Let's say that we want to find the acceleration of the particle at the instant t = 3 s.
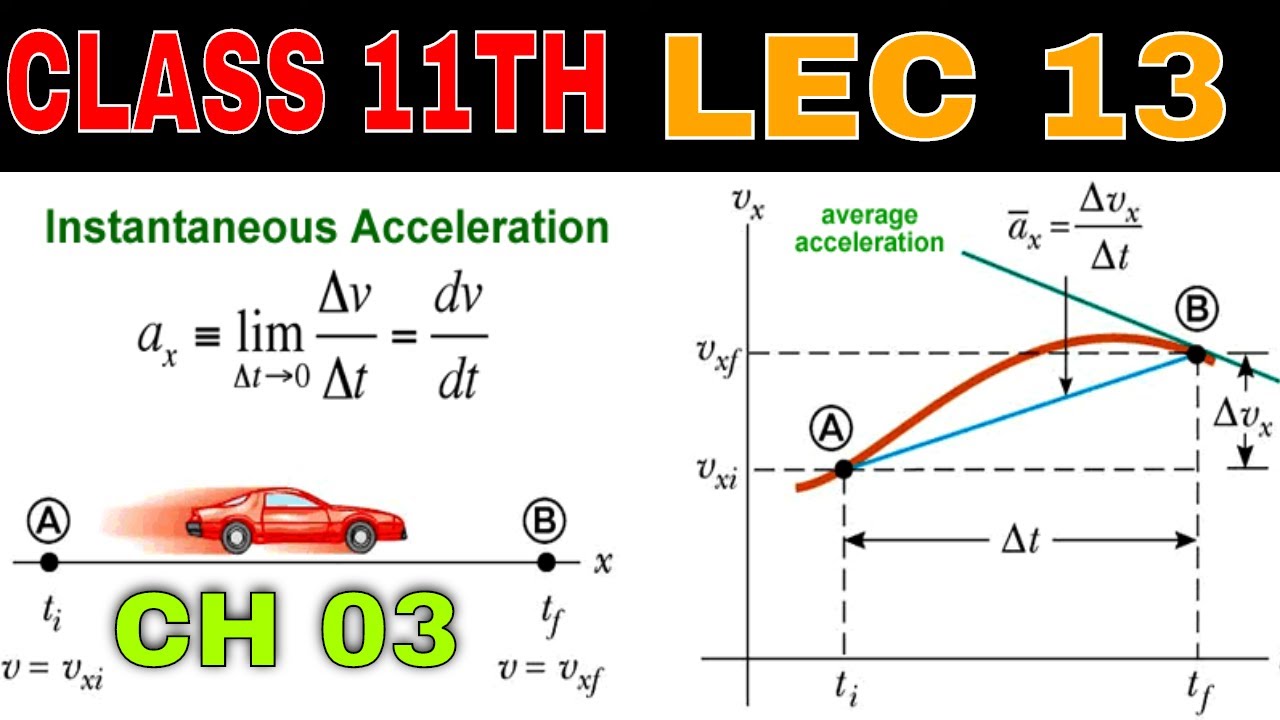
\begin{aligned}\vec{a} &= \dfrac{\vec{dv}}{dt}\\\end{aligned} the acceleration of an object at any instant of time is known as instantaneous acceleration. Since the instantaneous velocity can change with time, you will need a quantity that describes that change. Correct option is b) step1: So, the slope of a velocity vs.
Let us calculate the average velocity now for 5 seconds now.
Angular acceleration and angular velocity of a rigid body es ; At any time t the instantaneous acceleration is the rate of change of the velocity with respect to time. Instantaneous velocity is the calculation of velocity at any particular period, and acceleration is defined as the rate of change velocity(v) with consideration to a period. The same principle applies for
Solution for what is the instantaneous acceleration of a car at t = 3s with velocity v(t) = 2t²+3.
This quantity, the time rate of change of velocity with time, is called the acceleration, and it, too, is a vector. Acceleration is the rate which velocity changes over a time interval, or as you know, [itex]\frac {\delta v} {\delta s} [/itex]. In the case of uniform motion, average velocity over any time is the same as instantaneous velocity at any time. Velocity and acceleration of any point on a rigid body d.
Find the functional form of the acceleration.
V ( t) = d d t x ( t). The instantaneous center of velocity is a. Like average velocity, instantaneous velocity is a vector with dimension of length per time. In the limit of infinitesimally small time intervals, each velocity vector becomes the instantaneous velocity.
V ( t) = d d t x ( t).
Instantaneous acceleration of the body is always perpendicular to the instantaneous velocity. This is our definition of acceleration. Find the instantaneous acceleration at t = 1, 2, 3, and 5 s. Level 3 challenges instantaneous velocity the position (in meters) of an object moving in a straight line is given by s ( t ) = 4 t 2 + 3 t + 14 , s(t)=4t^2 + 3t + 14, s ( t ) = 4 t 2 + 3 t + 1 4 , where t t t is measured in seconds.
In general, the instantaneous velocity is the velocity of an object under the motion in a point of time.
We can show this graphically in the same way as instantaneous velocity. V ( t) = d d t x ( t). The si unit to represent the instantaneous velocity is m/s. Hi everybody here iam discussed about instantaneous speed and velocity in detail.
A body moving with uniform acceleration has a velocity of 11.5 cm/s when its x coordinate is 5.0 cm.
There is also average acceleration which equals a → = δ v → δ t, over some time δ t. The instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero, or the derivative of x with respect to t: In a similar manner from our lesson on velocity graphs, we'll look at the slope of the line in each region. Instantaneous acceleration is a → = d v → d t.
So, at 1 s the velocity is 2 m/s, at 2 s the velocity is 8 m/s, at 3 s the velocity is 18 m/s, etc.
Velocity of any point on a rigid body c. It is a vector quantity. Here iam also discussed about displacement time graph velocity time graph. Instantaneous acceleration is thus defined as the acceleration of an object at a specific instant of time let us look into the concept of instantaneous quantities with the help of an example firstly, we give a more formal mathematical approach of defining instantaneous quantities like instantaneous velocity, instantaneous acceleration etc
V = 2 t 2.
It is the slope of the. Instantaneous velocity at t = 5 sec = (12×5 + 2) = 62 m/s. When an object’s distance changes with time, its velocity is the rate at which the distance is changing with respect to time, while its acceleration is the rate at which the velocity is changing with respect to time. Here, our slope (rise over run) is the change in velocity divided by the change in time, or d v/ d t.
If we take the derivative of v inst with t, then we get acceleration.
Acceleration of any point on a rigid body b. Like average velocity, instantaneous velocity is a vector with dimension of length per time. A particle is in motion and is accelerating. Equation of velocity and acceleration.
The instantaneous acceleration of the ball at any time, t is given by the equation;
Time graph is the acceleration of the object at that interval. In a circular motion, the instantaneous acceleration of the body is always perpendicular to the instantaneous velocity, and that acceleration is called centripetal acceleration. As our time interval goes to zero, the velocity and acceleration of an object take on instantaneous values at a. So, if we have to find out the instantaneous velocity at t = 5 sec, then we will put the value of t in the obtained expression of velocity.
In physics, the instantaneous velocity is defined as the velocity of an object at the instant of time.
As for instantaneous velocity, it is, as the name suggests, the velocity on a specific time interval (in which we take [itex]t [/itex] to be infinitely close to [itex]0 [/itex]).