Instantaneous rate of change, or derivative, measures the specific rate of change of one variable in relation to a specific, infinitesimally small change in the other variable. The instantaneous rate of change is a measurement of a curve’s rate of change, or slope, at a certain point in time. The instantaneous rate is s’ in this situation (2).
PPT The DerivativeInstantaneous rate of change
F ( x) = 6 x 2 + 7 x − 5.
The relationship between the two is a function, denoted by f.
Instantaneous rate of change is like the speed your are driving your car at particular instant or any change occur at a particular instant or in a very very short interval of time as in case of speed that short interval is the amount of time you took to observe the speed in speedometer. It is the rate of change of a function at a specific point. Let’s suppose f is a function of x, then the instantaneous rate of change at the x = a will be the average rate of change over a short time period. Rate of change (technical analysis), a simple technical indicator in finance see also.
The rate of change at any given point is.
The instantaneous rate of change at a point is equal to the derivative function evaluated at that point. The instantaneous rate of change is the change in the concentration of rate that occurs at a particular instant of time. Rate of climb or rate of altitude change in aeronautics; While the average rate of change gives you a bird’s eye view, the instantaneous rate of change gives you a snapshot at a precise moment.
If given the function values before, during, and after the specified time, the instantaneous rate of change are often estimated.
Then if the average rate of change of. The derivative thus gives the immediate rate of change. Find the average rate of change of the. When a relationship between two variables is defined by a curve it means that the rate of change is always varying.
5 rows what is meant by instantaneous rate of change?
Instantaneous rate of change = lim h!0 1 = 1 squaring function f(x) = x2 average rate of change = f(x+ h) f(x) h = (x+ h) 2 (x) h algebra technique: S' (2) = 6 (2)² = 24 feet per second. The instantaneous rate of a reaction is the rate at which a chemical reaction is taking place at a given moment in time. Easy steps to use instantaneous rate of change calculator.
This is a very simple tool for instantaneous rate of change calculator.
Therefore, we can say that, in a function, the slope m of the tangent will give the instantaneous rate of change at a specific. So if we set h = a − x, then h 6= 0 and the average rate of change from x = a+h to x = a is ∆y ∆x = f(x)−f(a) x−a = f(a+h)−f(a) h. The instantaneous rate of change is that the rate of change of a function at a particular time. The instantaneous rate of change at some point x 0 = a involves first the average rate of change from a to some other value x.
F ( x) f (x) f (x) when.
The derivative f^\prime(a) is the instantaneous rate of change of y= f(x) with respect to x when x= a. In terms of the formula: It is a measure of the change in concentration of the reactants and the products at any specific time. The instantaneous rate of change is also the derivative f^\prime(x_1);
As you will learn, these rates can also be.
For example, how fast is a car accelerating at exactly 10 seconds after starting? Rate of change (mathematics), either average rate of change or instantaneous rate of change instantaneous rate of change, rate of change at a given instant in time; The instantaneous rate of change is the change in one variable, call it y, with respect to another variable, call it x. The instantaneous rate of change is another name for the derivative.
It is easy and simple to calculate the instantaneous rate of change of any function.
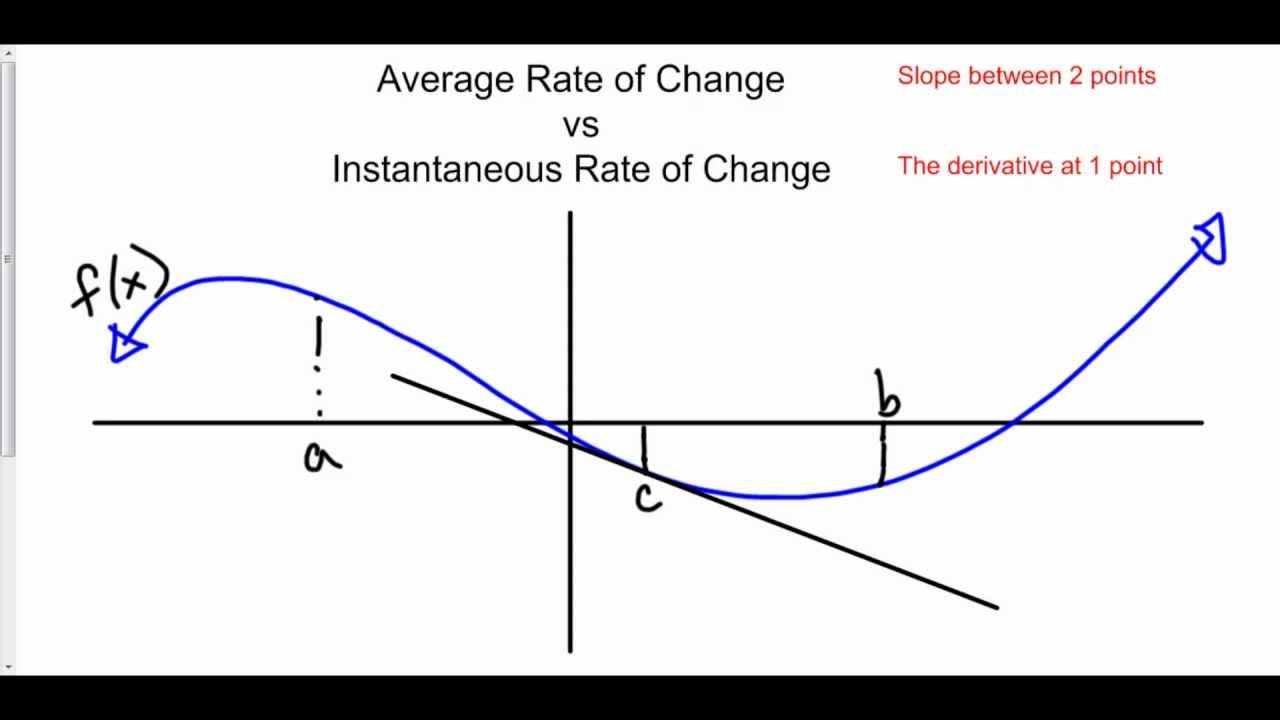
(5) a) at 3p.m., the plane was travelling at 750 km/h. The rate of change at one known instant or point of time is the instantaneous rate of change. Instantaneous rate of change de nition the instantaneous rate of change of function f at a, also called rate of change of f at a, is de ned to be the limit of the average rates of change of f over shorter and shorter time intervals around a. The average rate of change of a function can be determined with secant lines and the instantaneous rate of change can be determined with tangent lines.
Factor out = x2 + 2xh+ h2 x2 h = 2xh+ h2 h = h(2x+ h) h = 2x+ h instantaneous rate of change = lim h!0 (2x+ h) = 2x cubing function f(x) = x3 average rate of change = f(x+ h) f(x) h = (x+ h) 3 (x) h = x3 + 3x2h+ 3xh2 + h3 x3 h
It is equivalent to the value of the derivative at that specific point of time. The variation in the derivative values at a specific point also denotes the instantaneous rate of change. State if each situation represents average rate of change or instantaneous rate of change? Rate of change may refer to:
So we're trying to approximate the slope of the line tangent to f at f equals 7.
• lim x → a δ f. Rate = δ x δ t = 14 − 2 6 − 0 = 2 m/s.