Instantaneous acceleration is defined as acceleration at a y given point or at any instant of time. In simpler words, the instantaneous acceleration is the acceleration carried by an object at a specific time. When the acceleration that exists between two very close moments is discovered, the instantaneous acceleration is obtained.
PPT Chapter 2 PowerPoint Presentation ID1140003
Instantaneous acceleration a(t) is a continuous function of time and gives the acceleration at any specific time during the motion.
I need to find the acceleration at a specific time (for example, 6s).
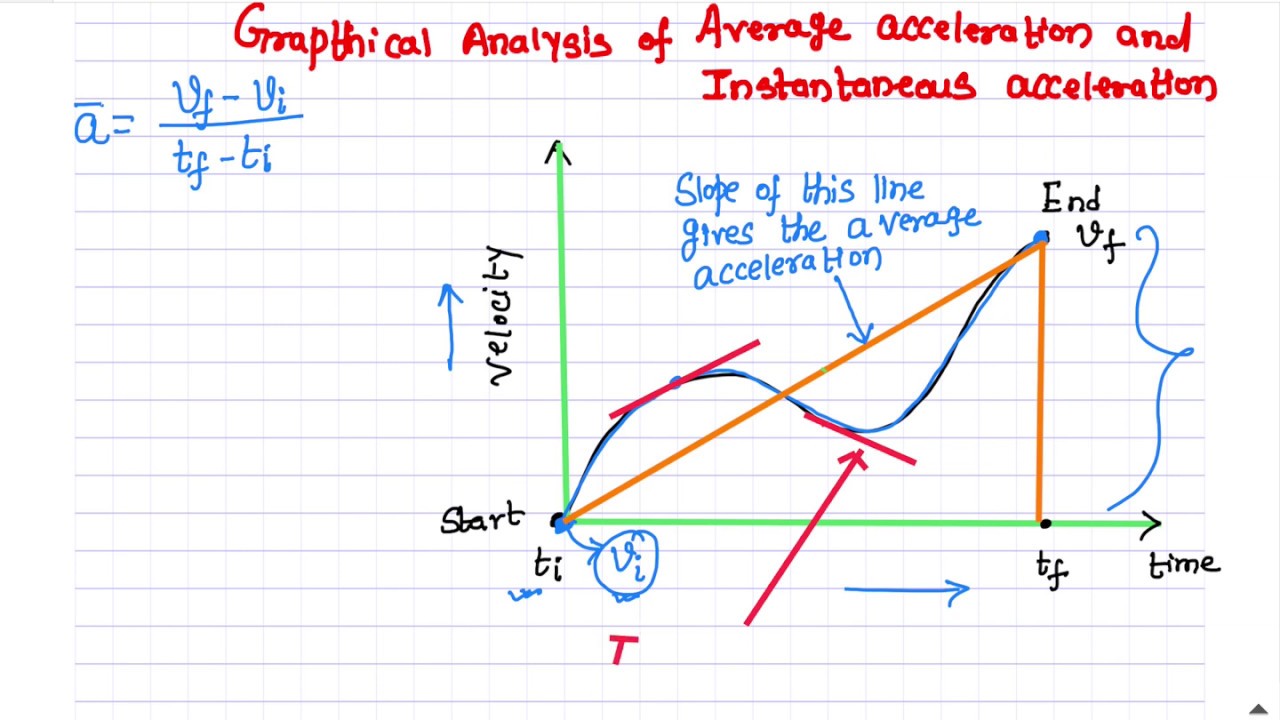
if at δ t time interval velocity if δ v then according to above defination ; At any time t the instantaneous acceleration is the rate of change of the velocity with respect to time. There is also average acceleration which equals $\vec{a}=\frac{\delta \vec{v}}{\delta t}$, over some time $\delta t$. At this point, instantaneous acceleration is the slope of the tangent line, which is zero.
Instantaneous acceleration, a a or the acceleration at a specific instant in time, is obtained by the same process as discussed for instantaneous velocity in the previous lesson on velocity and speed —that is, by considering an infinitesimally small interval of time.
It is calculated from the derivative of the velocity function. Instantaneous acceleration is the acceleration of the object at some discrete instant in time and can be found by taking the derivate of the velocity function. It is calculated from the derivative of the velocity function. The instantaneous acceleration is defined as the instantaneous rate of change of the velocity with respect to time.
Definition and formula for instantaneous acceleration.
The instantaneous acceleration of a body is the acceleration the body has at a particular time, at a specific point of its trajectory. Find v, then find a] Instantaneous acceleration is the acceleration of an object at a specific moment of time. To calculate instantaneous acceleration δ t → 0 hence, instantaneous acceleration a = l i m δ t → 0 δ t δ v = d t d v here d t d v differentiation of v with respect to time dt t which can be known.
(b) same as (a) but shown for instantaneous acceleration at minimum velocit.y otillustrate this concept, let's look at two examples.
Acceleration is the change in an object's velocity divided. How to calculate the instantaneous acceleration from a velocity vs time graph We represent the initial direction of motion as the +x direction. The average acceleration over a time interval 1 2 t tt ≤ ≤ is given by.
At any other time, the slope of the tangent line and thus instantaneous acceleration would not be zero.
It appears to be making step changes from one interval to the next, but in reality, there would be some line that connects each interval since it is really hard to have an instantaneous change in acceleration from one number to the next. In the case of uniformly accelerated motion, acceleration over any time is the same as instantaneous acceleration at any time. Instantaneous acceleration a, or acceleration at a specific instant in time, is obtained using the same process discussed for instantaneous velocity. The acceleration a that a particle has at an instant t is equal to the value that the average acceleration, calculated for an interval of time δ t which includes the instant t, approaches as the interval of time δ t gets smaller and smaller, i.e., as δ t approaches 0.
This means that the acceleration is not changing during the intervals.
Instantaneous acceleration a(t) is a continuous function of time and gives the acceleration at any specific time during the motion. We will use the general formula of average acceleration to find out the formula of instantaneous acceleration with the tweak of making the time elapsed nearly zero. Instantaneous acceleration, meanwhile, is the limit of the average acceleration over an infinitesimal interval of time. In other words, instantaneous acceleration, or simply acceleration, is the rate of.
To define the concept of instantaneous acceleration with precision we must begin with the average acceleration in an interval and make it infinitely small (.
Use the definition to find an expression for the instantaneous acceleration of an object moving with rectilinear motion according to the given function. This acceleration can be measured when the average acceleration that occurs between two very short instants (as close as possible to 0). Positive, negative and zero acceleration. = → = as acceleration is defined as the derivative of velocity, v, with respect to time t and velocity is defined as the derivative of position, x, with.
The acceleration of an object at any instant of time is known as instantaneous acceleration.
That is, we calculate the average acceleration between two points in time separated by δ t δ t and let δ t δ t approach zero. Instantaneous acceleration is the average acceleration between two points on the path in the limit that the time (and therefore the displacement) between the two points approaches zero.