Similarly, instantaneous angular acceleration is a measure for the instant change in angular velocity at a particular moment in consideration. Its the rate of change of velocity w.r.t time. The velocity change in instantaneous acceleration takes place at a specific time.
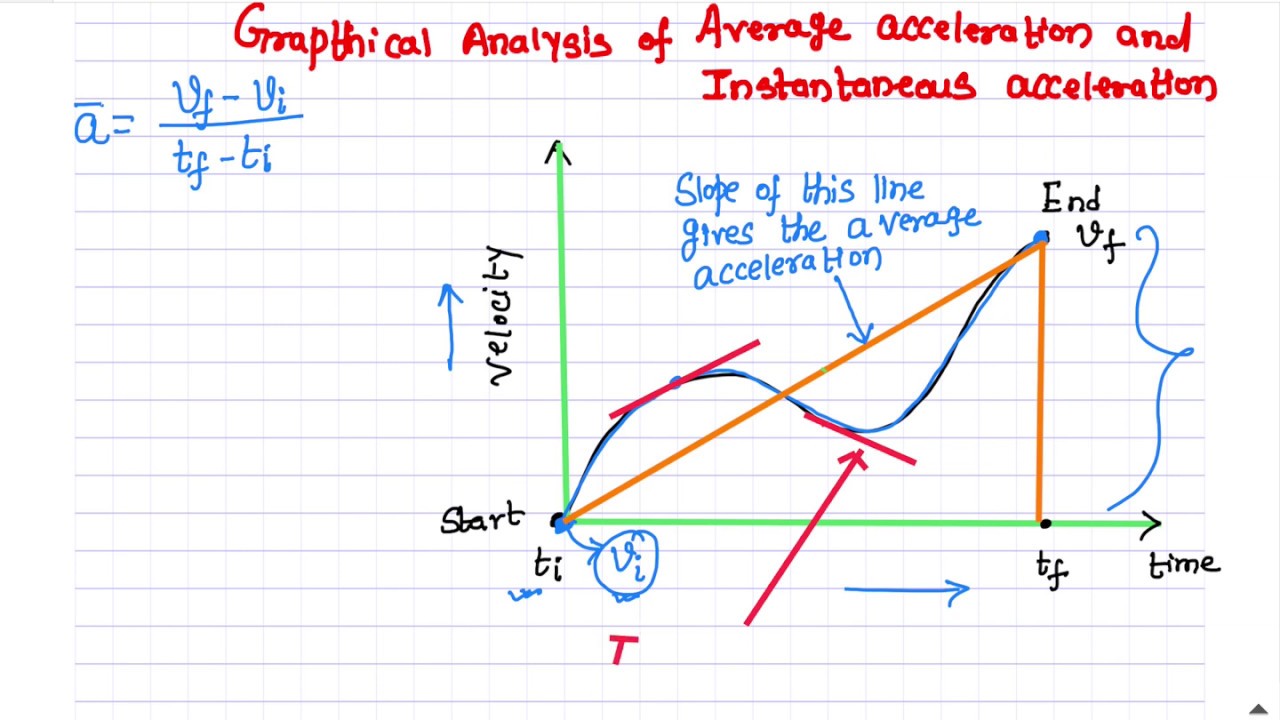
Graphical Analysis of Average acceleration and
Instantaneous velocity at t = 5 sec = (12×5 + 2) = 62 m/s.
This is the derivative of the velocity with respect to time:
When the object is moving with variable acceleration, then the object possesses different acceleration at different instant. It helps to measure the speed of a body along a specified route at any particular period t. V ( t ) = dx ( t )/ dt. Getting the equation or formula (step by step)
Instantaneous acceleration is the acceleration of an object at a specific moment of time.
In simpler words, the instantaneous acceleration is the acceleration carried by an object at a specific time. It can also be explained as the velocity derivative with respect to time. We will use the general formula of average acceleration to find out the formula of instantaneous acceleration with the tweak of making the time elapsed nearly zero. An object is moving right at that instant.
The instantaneous acceleration, or simply acceleration, is defined as the limit of the average acceleration when the interval of time considered approaches 0.
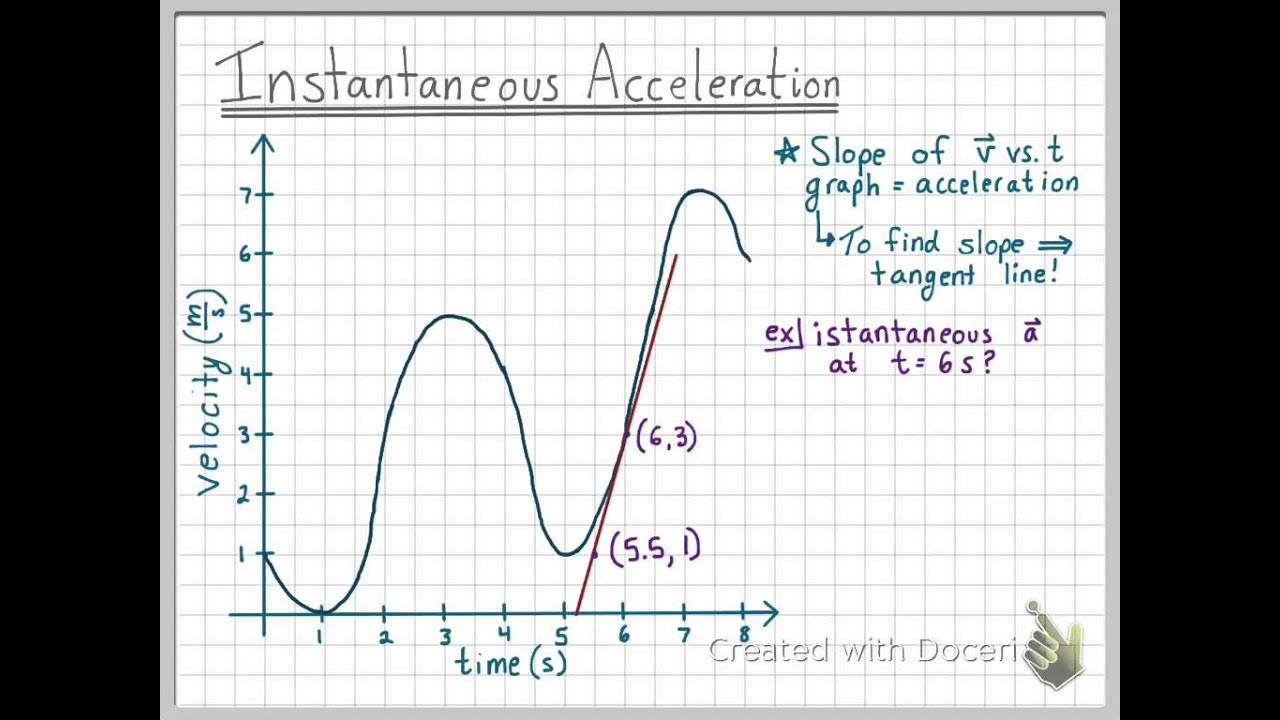
In view (a), instantaneous acceleration is shown for the point on the velocity curve at maximum velocity. Instantaneous acceleration is calculated as the average acceleration limit when a time interval attains zero. The instantaneous acceleration at any time may be obtained by taking the limit of the average acceleration as the time interval approaches zero. It is calculated from the derivative of the velocity function.
The acceleration of the object at different instant of time or at given time of motion, is called instantaneous acceleration.
When the acceleration that exists between two very close moments is discovered, the instantaneous acceleration is obtained. Definition the instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero, or the derivative of x with respect to t : Acceleration is the change in an object's velocity divided. Measure of distance traveled in a given period of time with a direction.
Instantaneous acceleration is then the limit of average acceleration as the time interval approaches zero — or alternatively, acceleration is the derivative of velocity.
Instantaneous acceleration is defined as the ratio of change in velocity during a given time interval such that the time interval goes to zero. The acceleration a that a particle has at an instant t is equal to the value that the average acceleration, calculated for an interval of time δ t which includes the instant t, approaches as the interval of time δ t gets smaller and smaller, i.e., as δ t approaches 0. The units for acceleration can be implied from the definition to be meters/second divided by seconds, usually written m/s 2. Terms used in the calculation:
This is thus, a vector quantity in physics.
In the terms of calculus , instantaneous acceleration is the derivative of the velocity vector with respect to time: This means that the acceleration is not changing during the intervals. Definition and formula for instantaneous acceleration. This acceleration can be measured when the average acceleration that occurs between two very short instants (as close as possible to 0).
Instantaneous angular acceleration (α (t)) gives the exact magnitude and direction of change of angular velocity at any point of time.
It is also defined in a similar manner as the derivative of velocity with respect to time. Instantaneous acceleration a(t) is a continuous function of time and gives the acceleration at any specific time during the motion. Instantaneous acceleration is the average acceleration between two points on the path in the limit that the time (and therefore the displacement) between the two points approaches zero. But in average acceleration, it is over a period of time.
Average acceleration is the average of the accelerations acquired in the whole journey by a body while instantaneous acceleration is the acceleration of the body at any particular instant of time.
Its the acceleration of an object at a particular instant/moment of time. For example velocity, instantaneous velocity is the velocity of a particular time in the presence of acceleration. You would typically get it from a position function that you've taken the time derivative of. S = (6t 2 + 2t + 4) velocity (v) = \ ( \frac {ds} {dt} \) = \ ( \frac {d (6t^2 + 2t + 4)} {dt}\) = 12t + 2.
An object moving at a constant speed and in a constant direction.
At this point, instantaneous acceleration is the slope of the tangent line, which is zero. Displacement/ position/ distance and time. So, if we have to find out the instantaneous velocity at t = 5 sec, then we will put the value of t in the obtained expression of velocity. X (t)=x0+v0*t + 0.5*a*t^2 => dx (t)/dt = v (t) = v0 + a*t.
Δ t = t 4 − t 3.
The term acceleration specifies the change in speed or velocity of a particle along the direction of path in an interval of time. Instantaneous acceleration, meanwhile, is the limit of the average acceleration over an infinitesimal interval of time.