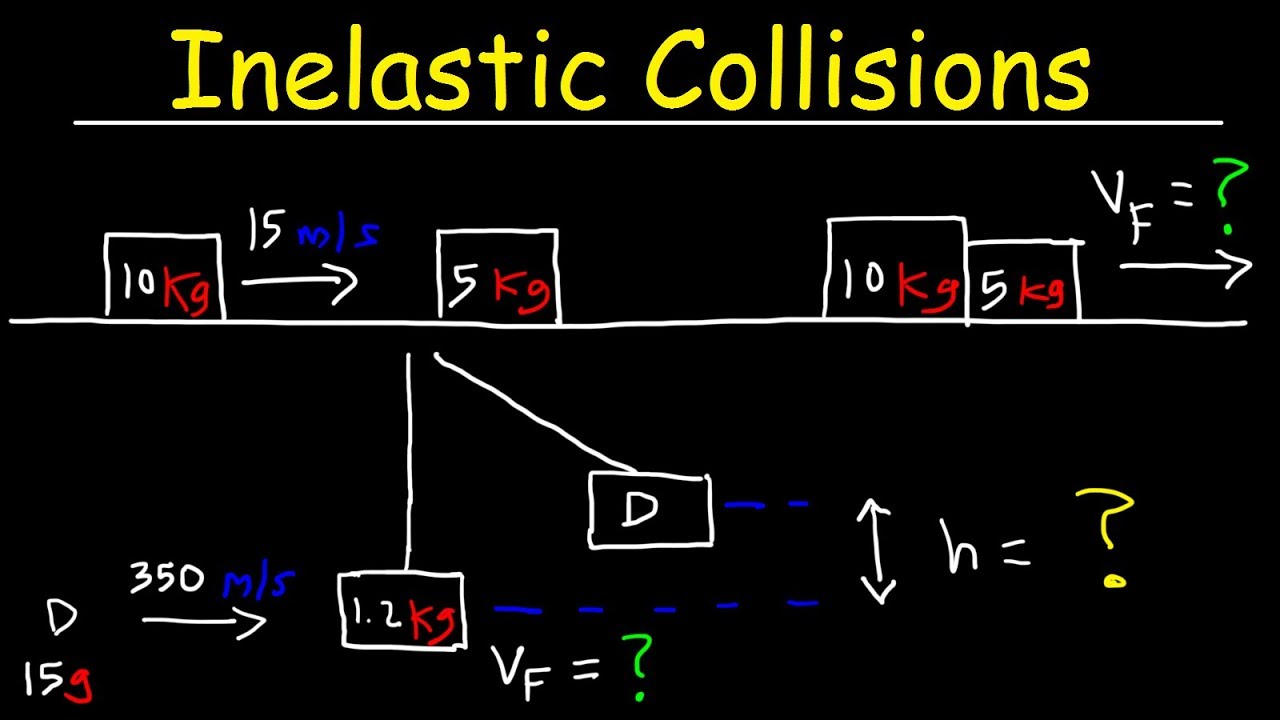
An additional equation needs to be introduced which accounts for the inelastic. In inelastic collision, there may be deformations of the object colliding and loss of energy through heat. Completely inelastic collision between two objects of equal mass
PPT Chapter 9 PowerPoint Presentation, free download
Therefore, the momentum p f after inelastic collision becomes m 1 v + m 2 v or v(m 1 +m 2) so, the equation of conservation of momentum for inelastic collision is, m 1 u 1 + m 2 +u 2 = v(m 1 +m 2) the formula for final velocity after inelastic collision is,
After all, if no external forces act on a system, its total momentum will be conserved.
To know, is momentum conserved in an inelastic collision, let’s first know collision. During an inelastic collision however, the momentum and the total energy of the isolated system are conserved. The final velocity for inelastic collision is articulated as. The momentum, {eq}\vec{p} {/eq}, of an object is the product of its mass and velocity:
Automobiles are designed to collapse and deform to absorb as much energy as possible (maximize the value of f) in a collision to protect the passengers.
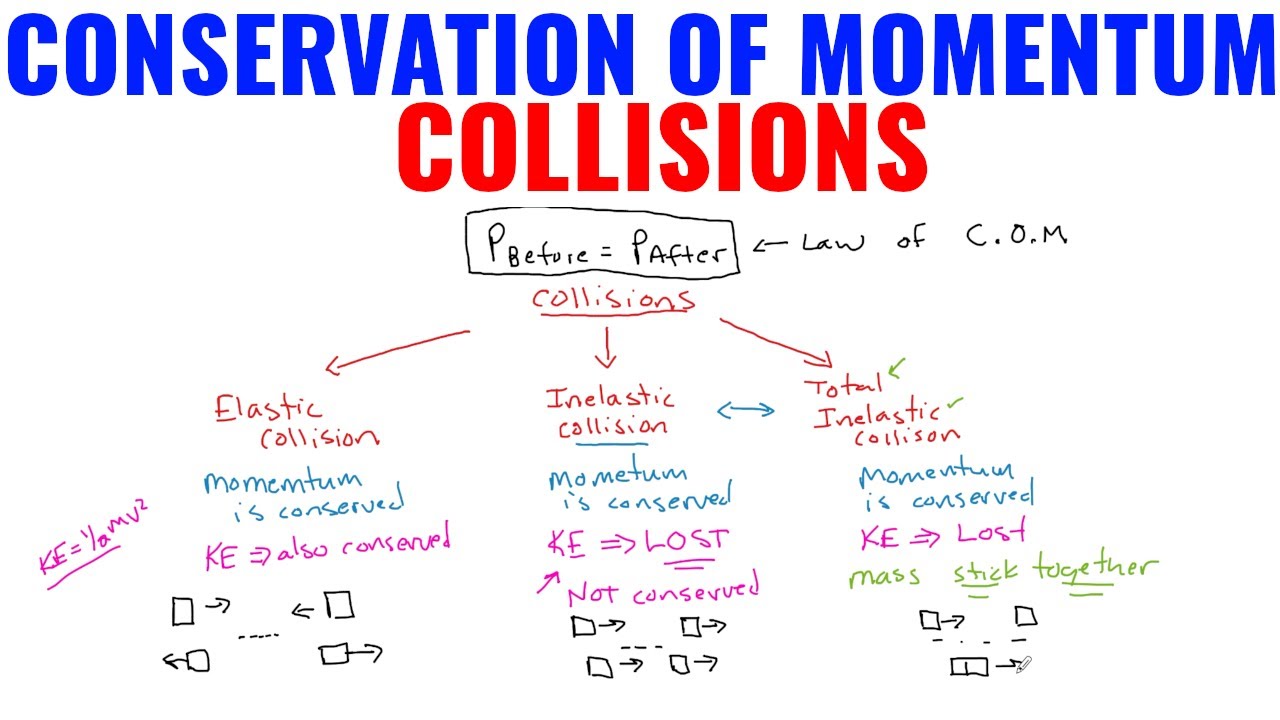
In inelastic collisions, the momentum is conserved but the kinetic energy is not. An inelastic collision is a collision in which total momentum is conserved but total kinetic energy is not conserved. So the total momentum before an inelastic collisions is the same as after the collision. The heat and the energy to deform the objects comes from the kinetic energy of the objects before collision.
From equation (1) for the conservation of linear momentum we have this equation can be expressed as its corresponding (scalar) equations along cartesian x , y , z directions:
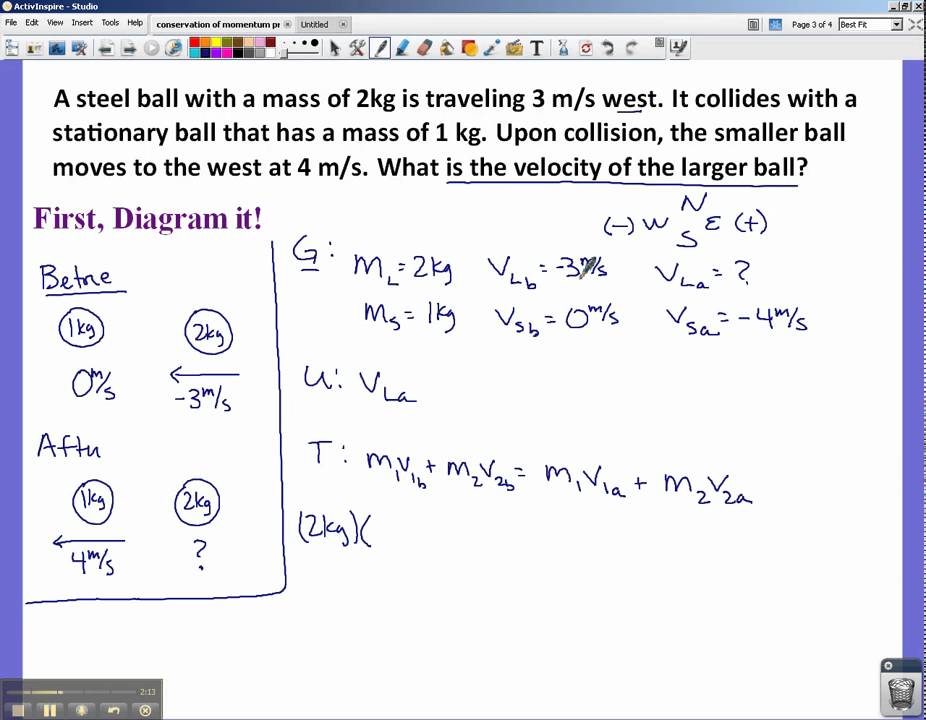
For collisions occurring in an isolated system, there are no exceptions to this law. Total momentum of the system (the two objects) before the collision is: I use the formula mass 1 x velocity 1. Suppose a chinese giant salamander chases a 5.00 kg carp with a velocity of 3.60 m/s to the
Momentum is conserved, but kinetic energy is not conserved.
In the case shown in this figure, the combined objects stop; When two bodies strike or collide, then the body’s kinetic energy is changed in the. This fact, together with conservation of momentum, allows the final motion of the two. Vocabulary for solving 1d inelastic collision problems momentum :
(b) the objects stick together, creating a perfectly inelastic collision.
The total system momentum is. This is not true for all. During an elastic collision, the momentum and the kinetic energy of an isolated system are conserved. The momentum lost by one object is equal to the momentum gained by another object.
Perfectly elastic collisions can happen only with subatomic particles.
When two bodies physically strike each other, or if their path of motion is influenced by each other, then we say it as collision. The standard method for handling inelastic collisions in one dimension is to invoke the law of conservation of momentum. The inelastic collision formula is made use of to find the velocity and mass related to the inelastic collision. In inelastic collisions, a part of the original kinetic energy is converted to some.
(a) two objects of equal mass initially head directly toward one another at the same speed.
Momentum is conserved, but internal kinetic energy is not conserved. E f = ½ (m 1 + m 2)v 2, e i = ½ m 1 u 1 2. An example of an inelastic collision is a car crash. The kinetic energy is transformed from or into other kinds of energy.
Numerical problems on collisions (elastic & inelastic collision) 1 ) a block of mass m 1 is at rest on a long frictionless table, one end of which is terminated in a wall.
(b) the objects stick together (a. V ′ =( m 1 m 1 + m 2 ) v 1. In this video i discuss what happens when two cars of different mass and same speed but in opposite direction collide. Collisions are of two types:
2.5fractional energy loss fractional energy loss f is one way to quantify the amount of energy “lost”[5] in a collision.
V ′ 2 sin θ 2 = −( m 1 v ′ 1 sin θ 1 ) m 2. Figure 8.7 shows an example of an inelastic collision. (a) two objects of equal mass initially head directly toward each other at the same speed. After an inelastic collision the two objects are stuck together, and thus travel with the same final velocity;
But if the collision is inelastic, both objects move with one final velocity v in the same direction.
P before = m 1 v 1 + m 2 v 2. An elastic collision and the other is an inelastic collision. M 1 u 1 = (m 1 + m 2)v. Inelastic collision between two particles general equations can be developed for the inelastic collision between two particles.
In an inelastic collision kinetic energy is not conserved, but momentum is conserved.
As discussed in a previous part of lesson 2, total system momentum is conserved for collisions between objects in an isolated system. Ask students to give examples of elastic and inelastic collisions. We start by assuming that fnet = 0, so that momentum p is conserved. Another block of mass m 2 is placed between the first block and the wall and set in motion to the left with constant speed v 2i.assuming that all collisions are completely elastic, find the value of m 2 for.
0 × 1 0 3 kg is traveling eastbound at + 24 m/s , +24\text{ m/s}, + 2 4 m/s , while a compact car with mass 1.0 × 1 0 3 kg 1.0 \times 10^3\text{ kg} 1.