Velocity of the moving object, in m/s. The final momentum of the first object is equal to 8 kg * 4 m/s = 32 n·s. Mass of the stationary object, in kg.
Momentum
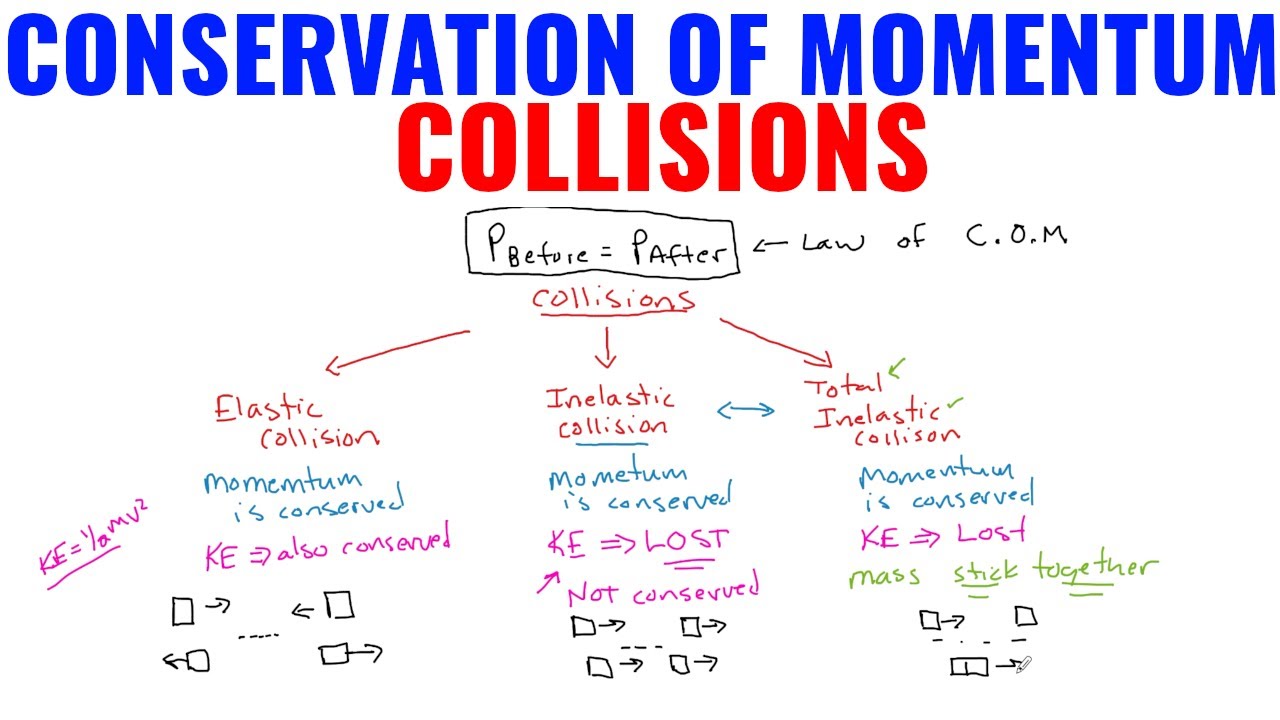
The crash in which kinetic energy of the system is not conserved but the momentum is conserved, then that collision is termed as inelastic collision.
All quantities are in si units.
Thus, it is possible to equate momentum in the start and final states of a system and thus calculate an unknown. After the boys collide, their combined velocity is 3.20 m/s. Calculate the momentum of the system before the collision. M 1 u 1 = (m 1 + m 2)v.
E f = ½ (m 1 + m 2)v 2, e i = ½ m 1 u 1 2.
The total system momentum is. So, the equation of conservation of momentum for inelastic collision is, m 1 u 1 + m 2 +u 2 = v(m 1 +m 2 ) the formula for final velocity after inelastic collision is, Pb = mass × velocity = 0.2 × 5 = 1 kg.m/s. M 1 v 1 + m 2 v 2 = ( m 1 + m 2) v ′, m 1 v 1 + m 2 v 2 = ( m 1 + m 2) v ′, 8.8.
Putting the value gives, m 1 u 1 + m 2 u 2 = (m 1 + m2) v.
P1 = pa + pb = 2 kg.m/s. Fill in the start conditions: The inelastic collision equation is: The total momentum of the system is the same after the collision as before it as shown by the equation initial momentum = final momentum (where final momentum is the sum of all momentums present in the system).
This simplifies the equation to.
Where v ′ is the velocity of both the goalie and the puck after impact. Mass and velocity of a. 2 = 0.1 × v1 + 0.2 × v2. (a) two objects of equal mass initially head directly toward one another at the same speed.
(b) the objects stick together (a.
That is, the total initial momentum of the system p~i is equal to the total final momentum p~f: An inelastic collisions occurs when two objects collide and do not bounce away from each other.momentum is conserved, because the total momentum of both objects before and after the collision is the same. Mass of the moving object, in kg. Inelastic collision formula when two objects collide with each other under inelastic conditions, the final velocity of the object can be obtained as;
In an inelastic collision kinetic energy is not conserved, but momentum is conserved.
Because the goalie is initially at rest, we know v2 = 0. We know that the formula for momentum is given as formula: Since the collision is inelastic, we know that. Momentum is conserved, m1→v i1 + m2→v i2 = m1→v f1 + m2→v f2 = (m1 + m2)→v f m 1 v → i 1 + m 2 v → i 2 = m 1 v → f 1 + m 2 v → f 2 = ( m 1 + m 2) v → f.
P2 the momentum of the two balls after collision is given by.
The calc will provide the unknown mass or velociy of b. Consequently, is momentum conserved in elastic and inelastic collisions? This formula is used to calculate the final velocity of the objects after the collision in one dimension if the collision is a perfectly inelastic collision. Velocity of the stationary object after collision, in m/s.
Mass of object 1 × initial velocity 1 + mass of object 1 × initial velocity 1 = (mass of 1 + mass of 2) × final velocity of combined objects) in.
In this case, initial momentum is equal to 8 kg * 10 m/s + 4 kg * 0 m/s = 80 n·s. The total momentum p~t of a system of n discrete parts can be expressed as the sum of each of the parts: Then fill in either the mass of b or the final velocity of a+b. The momentum and energy of the particle at rest are rr p =0 em=.
P~ t ˘m1 ~v1 ¯m2v~2 ¯¢¢¢¯mnv~n (2.2) when the sum of external forces acting on a system is zero, momentum is conserved.
We are required to determine the final velocity of the resulting mass, →v f v → f. To determine what is the final velocity in a perfectly inelastic collision, the concept of the conservation of momentum is used. Momenta are conserved, hence p1 = p2 gives. Where mass of body 1 = m 1.
The formula for inelastic collision:
According to the law of conservation of momentum, total momentum must be conserved. From, law of conservation of momentum we get to know that, p initial = p final The final velocity can be found for the two boys by rearranging the formula: For an inelastic collision, conservation of momentum is.
Mass of body 2 = m 2 the initial velocity of body 1 = u 1 the initial velocity of body 2 = u 2
P2 = 0.1 × v1 + 0.2 × v2. The inelastic collision formula is articulated as. In an elastic collision, both momentum and kinetic energy are conserved. Momentum is conserved, but internal kinetic energy is not conserved.
In any closed system, momentum is conserved.