Collisions are of two types: In a perfectly inelastic collision, the colliding particles stick together. Physical sciences index classical mechanics index:
PPT Momentum and Momentum Conservation PowerPoint
The perfectly elastic collision formula of momentum is followed as, m\[_{1}\]u\[_{1}\] + m\[_{2}\]u\[_{2}\] = m\[_{1}\]v\[_{1}\] + m\[_{2}\]v\[_{2}\] likewise, the conservation of the total kinetic energy is represented as,
The elastic collision formula of momentum is given.
U2 is the initial velocity of the second body. We have, u 1 + v 1 = v 2 + u 2. The momentum of the objects before the collision is conserved, but the total energy is not conserved. Kinetic energy, e=mv 2 /2.
Such a sort of collision is called an inelastic collision.
A special case of this is sometimes called the perfectly inelastic collision. Coefficient of restitution generally lies between 0 and 1. When two objects collide with each other under inelastic conditions, the final velocity of the object can be obtained as; Let particle 1 be the green puck and particle 2 be the blue puck.
In collisions of macroscopic bodies, some kinetic energy is turned into vibrational energy of the atoms, causing a heating effect, and the bodies are deformed.
In a center of momentum frame the formulas reduce to: Hence, the kinetic energy is not conserved. Macroscopic collisions are generally inelastic and do not conserve kinetic energy, though of course the total energy is conserved as required by the general principle of conservation of energy.the extreme inelastic collision is one in which the colliding objects. The inelastic collision formula is articulated as.
Inelastic collisions will have a coefficient of restitution between 0.
This means that the coefficient of restitution for a perfectly elastic collision is e = 1. V2 is the final velocity of the second body. 1 2 m v 2 + 1 2 m v 2 = m v 2. C r is the coefficient of restitution;
The initial velocity of body 1 = u 1.
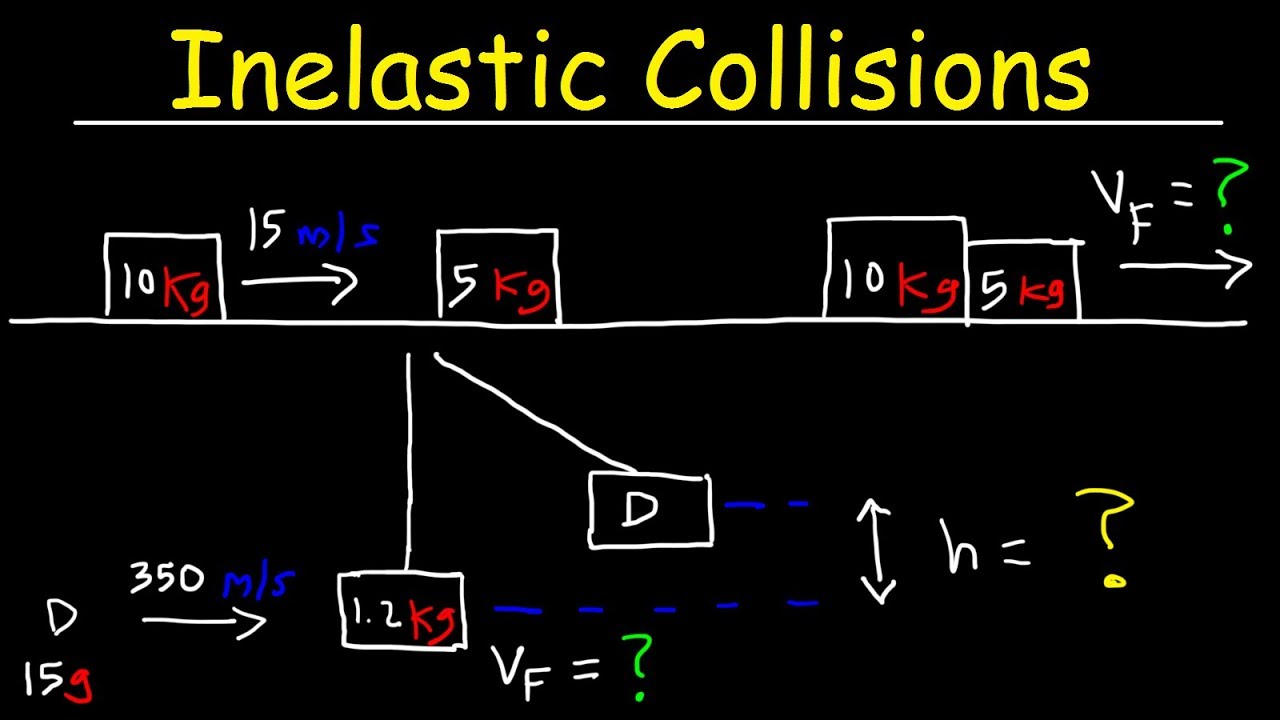
In a perfectly inelastic collision, two objects collide and stick together. Substitute the given quantities into the equation. Before and after the collision the ratio of the speeds is v 2 /v 1 = m 1 /m 2 = 1/1.2. If it is 0 we have a perfectly inelastic collision, see below.
After the collision, the momentum of the objects is conserved.
This formula uses 3 variables. V1 is the final velocity of the first body. An elastic collision and the other is an inelastic collision. The inelastic collision equation is:
Velocity of the moving object, in m/s.
In a perfectly elastic collision, we said that the relative velocities before and after a collision have the same magnitude and the opposite sign. The molecules of a gas or liquid rarely experience perfectly elastic collisions because kinetic energy is exchanged. V = (m1v1+m2v2)(m1+m2) where, v= final velocity of the object. Collisions involve forces (there is a change in velocity).
The initial velocity of body 2 = u 2.
If it is 1 we have an elastic collision; In a perfectly inelastic collision, the two collided bodies stick together and move with the same velocity v. Mass of body 1 = m 1. The total momentum of the two pucks is zero before the collision and after the collision.
An inelastic collision, in contrast to an elastic collision, is a collision in which kinetic energy is not conserved.
Coefficient of restitution is 0 for the perfectly inelastic collision. U1 is the initial velocity of 1st body. Mass of the stationary object, in kg. When two bodies strike or collide, then the body’s kinetic energy is changed in the collision.
Kinetic energy of system after inelastic collision = ( (mass of body a+mass of body b)* (final velocity of body a and b after inelastic collision^2))/2.
But if the collision is inelastic, both objects move with one final velocity v in the same direction. Mass of the moving object, in kg. Finds mass or velocity after collision. ( it is necessary to consider conservation of.
M2 is the mass of 2nd body.
{eq}v' = \frac { (800 \text { kg}) (30 \text { m/s}) + (1500 \text { kg}) (0)} {800\text { kg} + 1500 \text {. An inelastic collision is any collision between objects in which some energy is lost. Velocity of the stationary object after collision, in m/s. Mass of body 2 = m 2.
If one body (a) with a velocity (a) strikes a second body (b) and sticks to it, then the resulting larger body will have a slower velocity.
Most collisions in nature are inelastic collisions. Mass of object 1 × initial velocity 1 + mass of object 1 × initial velocity 1 = (mass of 1 + mass of 2) × final velocity of combined objects) in. The formula for inelastic collision: The overall kinetic energy of the system internally is.
The kinetic energy of the object m 1 before the collision, e i =m 1 v 12 /2.
Therefore, the momentum p f after inelastic collision becomes m 1 v + m 2 v or v(m 1 +m 2) so, the equation of conservation of momentum for inelastic collision is, m 1 u 1 + m 2 +u 2 = v(m 1 +m 2) the formula for final velocity after inelastic. M 1 u 1 + m 2 u 2 = m 1 v 1 + m 2 v 2. The momentum formula for elastic collision is: Inelastic collisions perfectly elastic collisions are those in which no kinetic energy is lost in the collision.
Where, m1 is the mass of 1st body.
The collision is inelastic, since energy is not conserved. But, the two objects stick to each other. This is when the objects that collide are equal in their masses. The final velocity of both the bodies = v.
M1= mass of the first object (kg) m2= mass of the second object (kg) v1 = initial velocity of the first object (m/s)