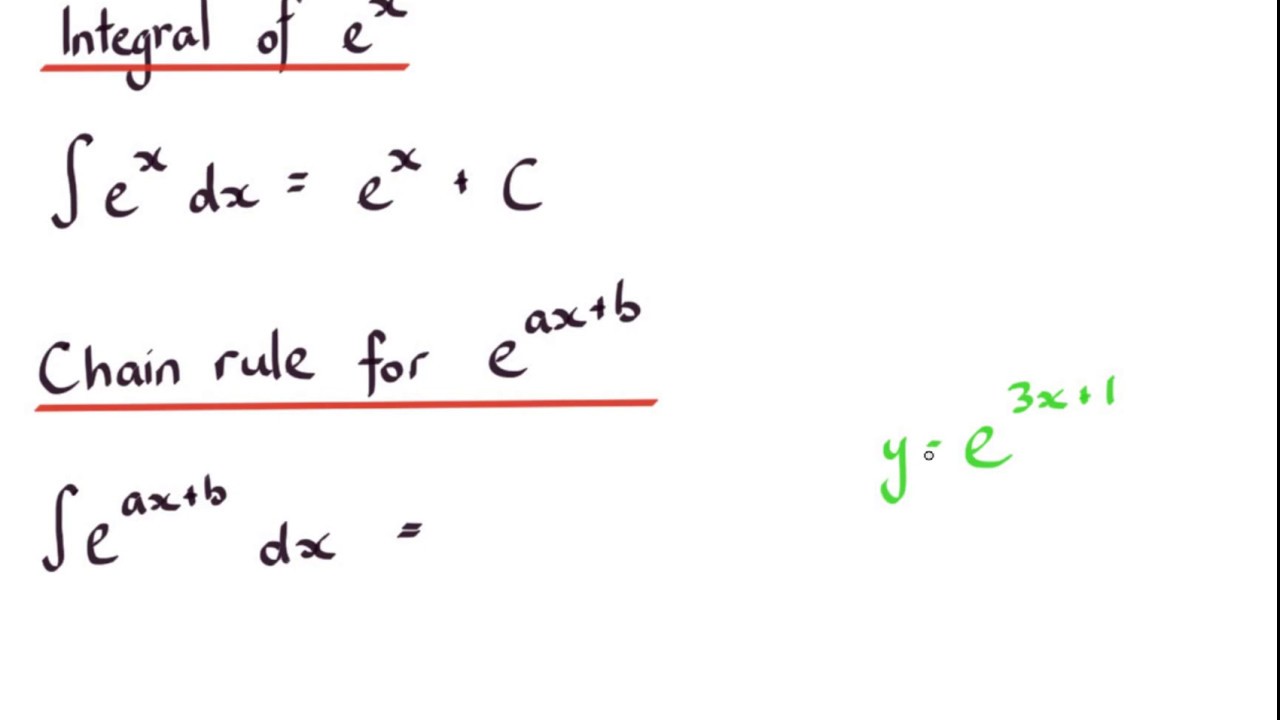| x + x 2 − a 2 | + c. And c gets cancelled out. For the following, let u and v be functions of x, let n be an integer, and let a, c, and c be constants.
PPT Indefinite Integral of Trig Functions PowerPoint
The integral of ex is ex itself.
\int _ { a } ^ { b } f ( y ) dx ∫.
We can differentiate this answer to check that we get e4x. Here, ∫ is the symbol of integration. ∫x.logx dx = ∫(logx)x dx. 1 4 eu + c = 1 4 e4x + c.
The first one is that you can apply limits after the end of your integrating result as you did in indefinite integration but make sure your variable is the same.
If n= 1 exponential functions with base a: E x (which is followed by dx) is the integrand. Thus, where ϕ(x) is primitive of […] We write it mathematically as ∫ ex dx = ex + c.
With the substitution rule we will be able integrate a wider variety of functions.
Integrals involving the error function in the following formulas, erf is the error function and ei is the exponential integral. So, for the given integral, let u = 4x. So, we can take it as; ∫ a b f ( y) d x.
Indeed, through the chain rule, the 1 4 we had to add gets undone by the 4 coming from the power of 4x via the.
Z ex dx= ex + c if we have base eand a linear function in the exponent, then z eax+b dx= 1 a eax+b + c trigonometric functions z Now calculate that at 1, and 2: This implies that du = 4dx. U = log x and dv = x dx.
Click here to see a detailed solution to problem 2.
Finding antiderivatives and indefinite integrals: Click here to see a detailed solution to problem 1. Let’s take an example of. ∫ 1 x 2 − a 2 d x = log e.
So with definite integrals we can ignore c.
Integration rules and formulas integral of a function a function ϕ(x) is called a primitive or an antiderivative of a function f(x), if ?'(x) = f(x). By integration by parts rule, we can solve the above integral; Fundamental rules ( ) 𝑥 First, let us take the inner integral on the functions ∫x.logx dx.
The integral of reciprocal of the square root of difference of squares is equal to the sum of natural logarithm of sum of variable and square root of difference of squares, and the constant of integration.
Evaluate the integral ∫5 sinx dx Indefinite integrals of sin (x), cos (x), and eˣ. So, du = (1/x) dx.v = x 2 /2 ∫ 2x dx = 22 + c.
Evaluate the integral ∫x 5 dx solution:
Integration rules and techniques antiderivatives of basic functions power rule (complete) z xn dx= 8 >> < >>: Z ax dx= ax ln(a) + c with base e, this becomes: K f(x) ∫k f(x) dx = k ∫f(x) dx example: (2 2 + c) − (1 2 + c) 2 2 + c − 1 2 − c.
Common integrals ∫k dx k x c= + 1 1 1 nn,1 n x dx x c n+ + ∫ = + ≠− 1 1 ln x dx dx x c x ∫∫− = = + 1 11 ln ax b a dx ax b c + ∫ = ++ ∫ln lnudu u u u c= −+( ) ∫eeuudu c= + ∫cos sinudu u c= + ∫sin cosudu u c− += ∫sec tan2udu u c= + ∫sec tan secu udu u c= + ∫csc cot cscu udu u c−+= ∫csc cot2udu u c− =+ ∫tan lnsecudu u c= +
Therefore, using equation (2), we get. 4 − 1 + c − c = 3. This is the currently selected item. One way to find the integral of x e x is to use the product rule and then integrate.
Let f(x) be a function.
∫e4xdx = 1 4∫e4x ⋅ 4dx = 1 4 ∫eudu = 1 4eu +c. The logarithmic function on the x function with another function x is not integrated directly. E x [f (x) + f ’ (x)]. The integration of exponential functions.
Then the collection of all its primitives is called the indefinite integral of f(x) and is denoted by ∫f(x) dx.
This is how the integration by parts formula is derived. The integrals in this section will all require some manipulation of the function prior to integrating unlike most of the integrals from the previous section where all we really. F(x) = x n ∫x n dx = x n + 1 / (n + 1) + c example: Common integrals indefinite integral method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − integrals of rational and irrational functions 1 1 n x dx cn x n + = + ∫ + 1 dx x cln x ∫ = + ∫cdx cx c= + 2 2 x ∫xdx c= + 3 2 3 x ∫x dx c= +
A definite integral is used to compute the area under the curve these are some of the most frequently encountered rules for differentiation and integration.
If n6= 1 lnjxj+ c; Xn+1 n+ 1 + c; ∫ 2x dx = 12 + c. Click here to see a detailed solution to problem 3.
Rules for solving integration by parts for definite integral limits.
We will use the integration rule for ex: