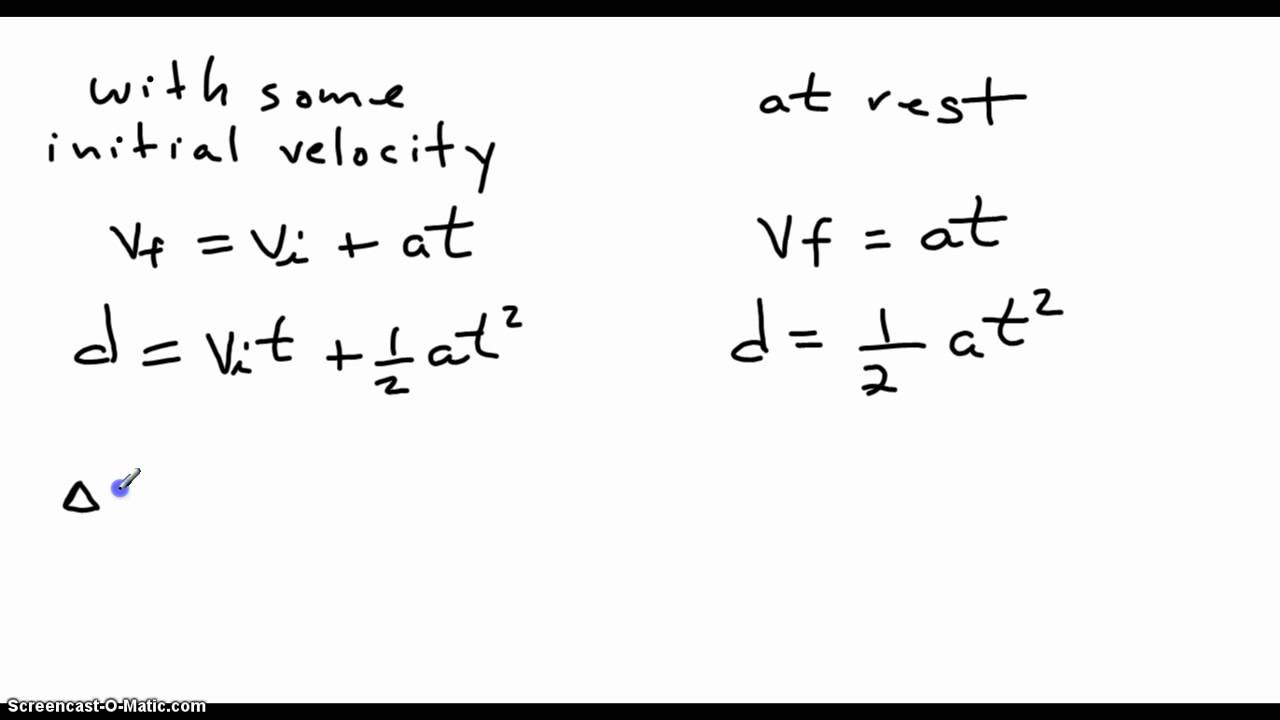Includes displacement , time interval , initial velocity , final velocity , and acceleration. Acceleration approaches zero in the limit the difference in initial and final velocities approaches zero for a. The following are the three equation of motion:
suvat Equations of Motion for Constant Acceleration YouTube
V = v 0 + a ⋅ t
These equations are valid only when the acceleration is constant.
Third equation of motion : Formula that describes the relationships between kinematic variables when acceleration is. In part (a) of the figure, acceleration is constant, with velocity increasing at a. S = u t + 1 2 a t 2.
Kinematic equations for uniformly accelerated motion.
The results of this case are summarized below. The object has two forces acting on it, both of which are inversely proportional to the square of the distance from r_0. A = v2 − v20 2(x − x0). An object of mass m is travelling from a point r_0.
Acceleration may be positive or negative, depending on how velocity changes.
Position of object at time t=0 is 0. V 2 = u 2 + 2 a s. These equations are used to solve problems related to straight line motion with constant acceleration. Class 11 physics motion in a straight line.
Department of physics and applied physics 95.141, spring 2014, lecture 3 lecture 3 chapter 2 equations of motion for constant acceleration 01.29.2014
6/1/20 objective the objective of this was to simulate a car accelerating down a road. Note that distance is always a positive quantity. To brush up on the basics of motion, refer the article listed below:: Note that speed is always a positive quantity.
These equations of motion of a moving particle with constant acceleration a are.
Here, v 0 is the initial [ [velocity]] of the particle and. V = v0 + at. V aa a t vv a t t v v at t. Our objective is to derive 4 equations called the kinematic equations of motion that can be used to describe any object moving with constant (uniform) acceleration in 1d.
For example, if you steadily increase your velocity (that is, with constant acceleration) from 30 to 60 km/h, then your average velocity during this steady increase is 45 km/h.
(constant acceleration) 0 ( ), 0 0 and t t t v t v by definition acceleration a o t v t v a o the velocity is increasing at a constant rate v 0 v t v(t) v o at (1) velocity equation since a=const, v is a straight line and it doesn’t matter which acceleration to use, instantaneous or average. Note that velocity has the same sign as displacement. ∆ = = = ∆ − = − (figure) illustrates this concept graphically.
Figure illustrates this concept graphically.
Constant acceleration motion equations the equations of the constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m.) are: Position of object at time t=0 is x 0. Second equation of motion : Constant translational acceleration in a.
Thus, for a finite difference between the initial and final velocities acceleration becomes infinite in the limit the displacement approaches zero.
We need to be able to analyze the motion of such objects. There are 3 kinematic equations of rectilinear motion for constant acceleration. The main focus of the study was on the position and velocity of the car. The differential equation of motion for a particle of constant or uniform acceleration in a straight line is simple:
If we let ti = 0 and tf = t, we get ax = vxf vxi t:
V = v 0 + a t. First equation of motion : Solving for vxf we get an expression for the nal velocity in terms of the initial velocity, the acceleration, and the time V = u + a t.
V 2 = v 0 2 + 2 a ( x − x 0) or sometimes written as, v 2 = v 0 2 + 2 a d.
X = x 0 + v 0 t + 1 2 a t 2 or sometimes written as, d = v 0 t + 1 2 a t 2. The acceleration is constant, so the second derivative of the position of the object is constant. The equations of straight line motion with constant acceleration are equation \eqref{2}, equation \eqref{6}, equation \eqref{8} and equation \eqref{9}. Size 12 {v} {} is just the simple average of the initial and final velocities.
Kinematic equations for uniformly accelerated motion.
This experiment was done using the standard equation of motion.