S = u t + 1 2 a t 2 third equation of motion : S = 1 2 × ( u + v) × ( t) − − e q u a t i o n ( a) substituting the value of the final velocity from the first equation and simplifying, we get. S = ut + (1/2) at 2 and v 2 = u 2 + 2as and these can be derived with the help of velocity time graphs using definition acceleration.
Physics Matric Part 1 First Equation of Motion Physics
V = u + at.
These equations are called equations of motion.
This is the first equation of motion. V = u + at. So, our first equation of motion is. Using equation (1) if we replace t we get, s = 1 2 x ( v + u) x ( v − u) a.
Equations of motion in this lesson we introduce equations of motion.
Accelerated motion, but do not use them in the derivation of these relationships. We will try to derive the three equations of motion one by one. V = final velocity of the body. Derive equation of motion graphically for a particle moving with initial velocity and.
Using the same equation (2), s = 1 2 x (v + u) x t.
First equation of motion : V = u + at; V 2 = u 2 + 2 a s The following are the three equation of motion:
This graph has 3 stages.
There were also several instances where graphical relationships were interwoven with other techniques to arrive at the equations. Since r q = ( v − u) and p r = o s = t. Substituting various values we get. Let’s start with first equation of motion.
The third equation of motion relates to velocity, displacement, and acceleration.
S = u t + 1 2 a t 2. Final velocity of the body (v) = bc. Or, s = u × t + 1 2 a t × t. S = u × t + 1 2 ( v − u) × t.
The rate of change of velocity is acceleration, a = dv / dt.
Be = ab + ae. S = ut + third equation of motion : Second equation of motion : Equations of motion by graphical system.
Let's derive the three equations of motion using a velocity time graph v = u + at s = ut + 1/2 at^2 v^2 = u^2+2as.
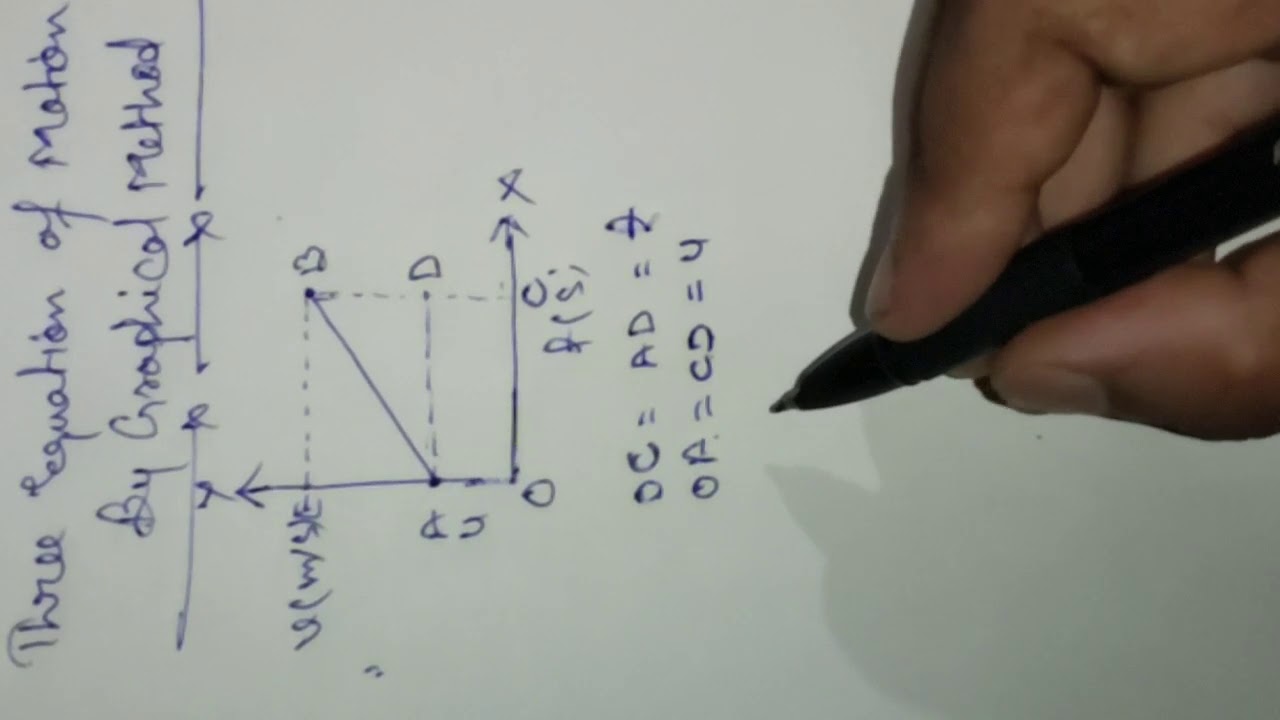
(2) by substituting dc from (2) in (1): (1) derivation of v=u + at. Initial velocity of the body (u) = oa. Where u = initial velocity of the body.
V = at + u.
Equation of motion by graphical method. We show how the graphs of motion and the basic definition of velocity can be used to develop the four equations of motion. From the graph bc = bd + dc. The object has a uniform acceleration.
V = u + a t second equation of motion :
S = ( v 2 − u 2) 2 a. Velocity changes from a to b in time t (uniform acceleration a) final velocity v=bc. The speed of the particle is minimum at time. V = u + at.
When an object moves along a straight line with continuously changing acceleration, it’s possible to relate its velocity(or you can say speed), acceleration while changing its position, and the distance covered by it in a particular time that is described by three given.
Let's derive all 3 equations First equation of motion : (2) derivation of s = ut +1/2 x at2. Motion class 9 physics with ved tutorials by vineet sir keep subscribe my class
V 2 = u 2 + 2 a s.
Three equations of motion are v = u + at; Let, oe = time (t) from the graph: Velocity (v) of a particle moving along a straight line varies with time (t) as v = t 2 − t, where v is in m/s and t' is in seconds. Since ( v − u) = a t.
V = dc + od (qab = dc & ae = od) v = dc + v [qod = u] v = dc + v.
Where, v = final velocity, u = initial velocity, a = acceleration and. A = uniform acceleration of the body. Therefore, v = bd + dc This is the second equation of motion.
Let's derive the three equations of motion using a velocity time graph v = u + at s = ut + 1/2 at^2 v^2 = u^2+2as.
Equations of uniformly accelerated motion present in. (3) derivation of v2 = u2 + 2as. Dear students equations of motion are used in uniform accelerated motion.there are three equations of motion.first equation is related to final velocity of. The equations of motion represent the relationship between an object's acceleration, velocity and distance covered if and only if, the object is moving on a straight path.
This is how you derive the second equation of motion by graphical method.
If you're seeing this message, it means we're having trouble loading external resources on our website. First equation of motion : Initial velocity u at a =oa. S = 1 2 × ( u + u + a t) × ( t) ⇒ s = 1 2 × ( 2 u t + a t 2) ⇒ s = u t + 1 2 a t 2.