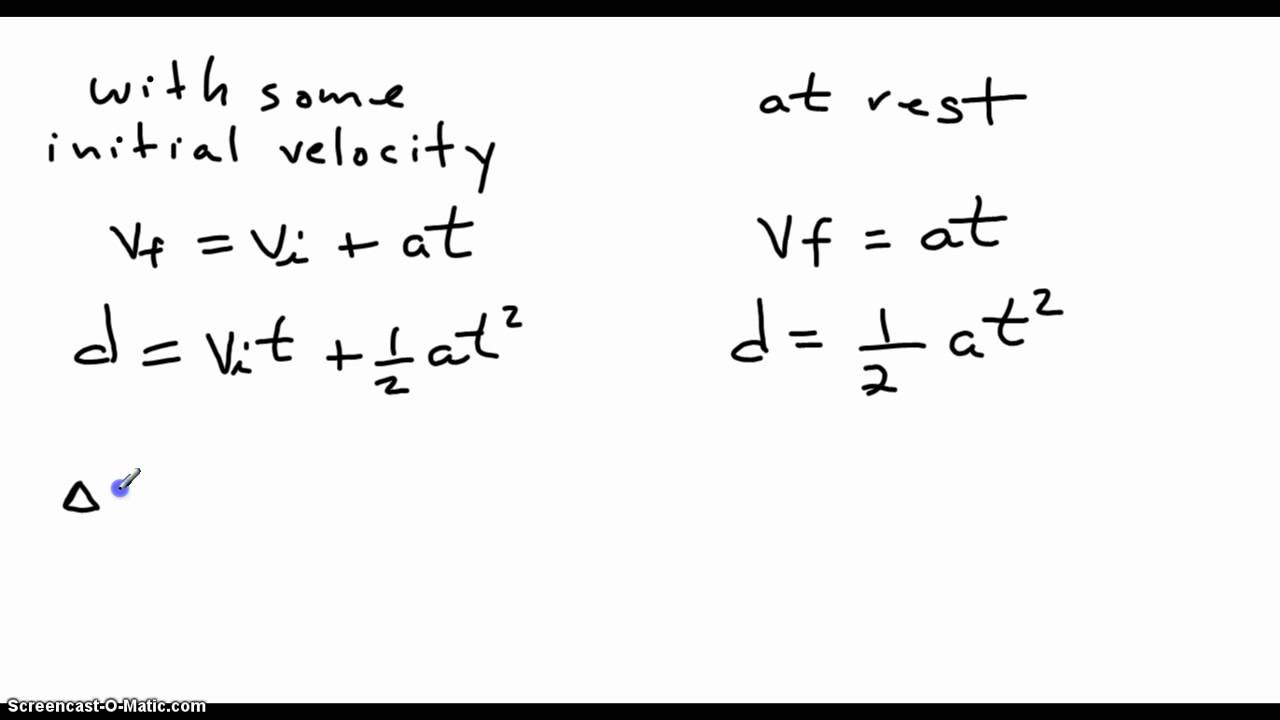Any of four equations that apply to bodies moving linearly with uniform acceleration (a). Let, oe = time (t) from the graph: Up to 24% cash back the 5 key equations of accelerated motion apply to motion with uniform acceleration.
Equations for Motion under Constant Acceleration YouTube
The equations of the constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m.) are:
Velocity of the body at a given time ( v) and at the initial time ( v0 ).
This is the second equation of motion. V = u + a t. V = ½ [ ( v0 + at ) + v0] v = ½ (2 v0 + at) v = v0 + ½ at [b] now substitute [b] into [a] to eliminate v [vee bar]. When an object moves along a straight line with uniform acceleration, we can relate its velocity, acceleration and distance travelled in a particular time with a set of equations.
∴ s = area of the quadrilateral opqs.
$s = ut + \dfrac{1}{2}a{t^2}$ c. Let on object on moving in uniform accelerationu= initial velocity of objectv= final velocity of objecta= uniform velocity of objectlet object reach point b other time (t)slope =acceleration (a) = timechange in velocity change in velocity ab= vˉ− uˉtime ad=t∴ a= tv−u , or v=u+at. And finally, solve for s as a function of t. Position of the body at a given time ( x) and at the initial time ( x0 ).
Up to 24% cash back 1.
$v = u + at$ b. Let the velocity at time (t = 0) and t be u and v respectively. When solving uniform acceleration choose which equation(s) to use based on the given and required variables for the question. S = s0 + ( v0 + ½ at) t.
A = v2 − v20 2(x − x0).
The acceleration is constant, so the second derivative of the position of the object is constant. Five key equations for motion. We are familiar with the concept of uniform motion, if an object covers equal displacement in an equal interval of time it is said to be undergoing uniform motion. The kinetic equation of motion under gravity can be obtained by replacing ‘a’ by ‘g in the of motion [obtained earlier.
∴ v = u + at.
Solving problems using equations of motion for uniform acceleration how far. V = u + at. Acceleration approaches zero in the limit the difference in initial and final velocities approaches zero for a. Use standard gravity, a = 9.80665 m/s 2, for equations involving the earth's gravitational force as the acceleration rate of an object.
Oc = v and oe = da = t.
S = ut + at 2 /2. The results of this case are summarized below. V = u ± gt; The kinematic formulas are a set of formulas that relate the five kinematic variables listed below.
Third equation of motion :
Equations of motion under gravity are as below: If we know 3 of these 5 kinematic variables for an object under constant acceleration, we can use a kinematic formula (seen below) to solve for one of the unknown variables. Equations 1 through 4 are the key equations used to solve for variables in this calculator however you will sometimes see a different number of uniformly accelerated motion equations depending on the resource. The equations, which relate distance covered (s) to the time taken (t), are:
Constant translational acceleration in a straight line
(1) this is the first equation of motion. Thus, for a finite difference between the initial and final velocities acceleration becomes infinite in the limit the displacement approaches zero. The slope of line pq gives the acceleration. The motion of an object falling freely under gravity is, thus, a case of motion with uniform acceleration.
V 2 = u 2 + 2as
There are three equations of motion that are as listed below: The fourth equation ⇒ this links velocity, acceleration and displacement. They involve the variables for displacement, initial velocity, final velocity, acceleration, and time interval. V = ½ (v + v0) [4] substitute the first equation of motion [1] into this equation [4] and simplify with the intent of eliminating v.
V = u + at s = (u + v)t/2 s = ut + at 2 /2 v 2 = u 2 + 2as where u is the initial velocity of the body and v is its final velocity.
Let after time “t” its final velocity becomes “v” due to uniform acceleration “a”. Write three equations of uniformly accelerated motion relating the initial velocity $\left( u \right)$, final velocity $\left( v \right)$, acceleration $\left( a \right)$ and displacement $\left( s \right)$. The second equation ⇒ displacement = average velocity x time ⇒ the average velocity is half way between the initial and final velocities. V = u + at.
Distance traveled = average velocity × time.
Derive the following equations for a uniformly accelerated motion: Combined with the statement that for uniform acceleration the average speed is jus t half the sum of the beginning and ending speeds to arrive at one of the underlying equations describing uniformly accelerated motion. Be = ab + ae These equations are called equations of motion.
The distance traveled by moving body in time ‘t’ is ‘s’ then the average velocity = (v + u)/2.
The differential equation of motion for a particle of constant or uniform acceleration in a straight line is simple: Its unit in the international system (si) is the meter (m) v, v0: Suppose a body has an initial velocity ‘u’ and uniform acceleration ‘a’ for time ‘t’ so that its final velocity becomes ‘v’. Conceptual textbooks, by their very nature, do not neces sarily
View copy of 2.1 notes day 4.docx from phys ib at regent university.
S = (u + v)t/2.