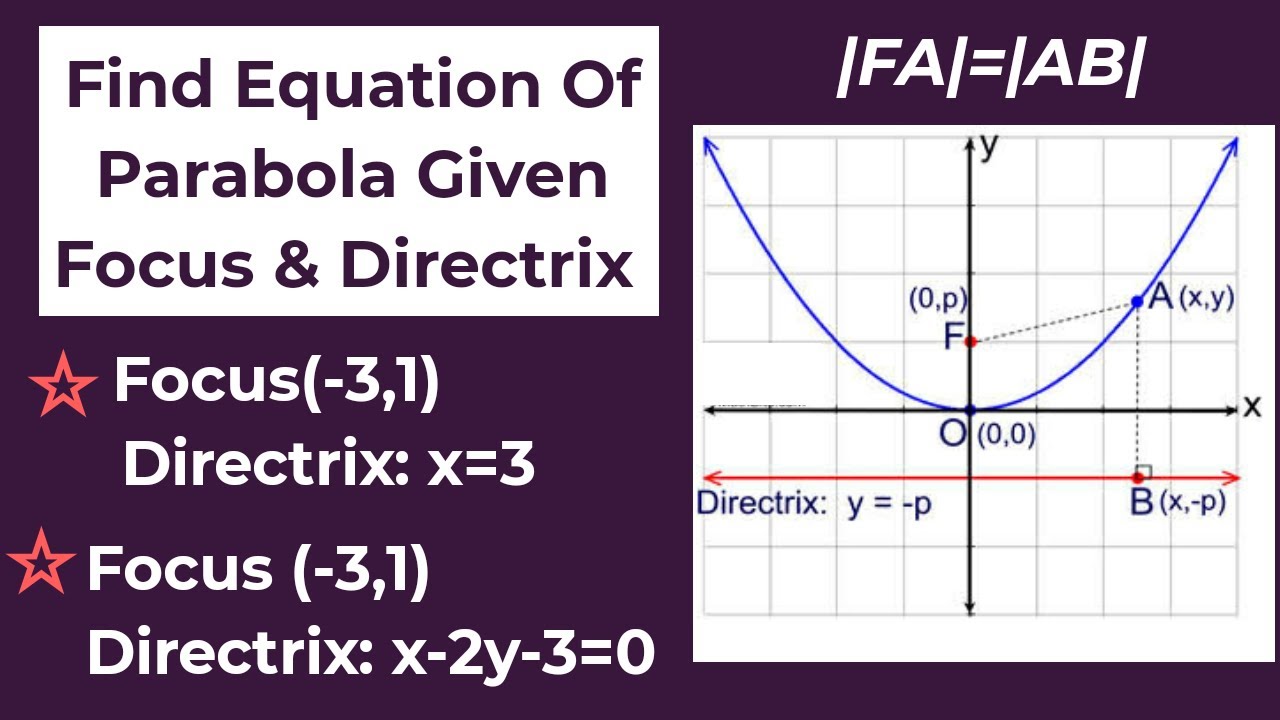
The basic definition of a parabola is a locus of all points such that the point in the locus is equidistant to a fixed point and to a line, called the. If the parabola opens up or down the equation is: I.e x = 3 is the required equation for directrix.
The equation of the directrix of the parabola whose vertex
For a fixed point, called the focus, and a straight line, called the directrix, a parabola is the set of points so that the distance to the focus and to the directrix is the same.
Up to 10% cash back if f is the focus of the parabola, v is the vertex and d is the intersection point of the directrix and the axis of symmetry, then v is the midpoint of the line segment f d ¯.
If p is any point on the parabola then p is equidistants from s and d In this example the focus is at (4, 3) so k + p = 3. Up to 10% cash back therefore, the equation of the parabola with focus ( a , b ) and directrix y = c is ( x − a ) 2 + b 2 − c 2 = 2 ( b − c ) y Learn how to find the equation of a parabola given the focus and directrix in this free math video tutorial by mario's math tutoring.0:10 what is a parabola0.
First note that you have p = 3, q = 6, and r = 4.
So a = 12/4 = 3. To find the equation of the parabola: The focus is located at (h, k + p). The answer part 5) is.
The graph is shown in the figure attached.
The fixed point is called the focus and the line is the directrix. The distance from a point of the parabola to. Any point (x,y) on the parabola is equidistant from the directrix and the focus. The equation for a parabola curve can be found from the focus and directrix.
Let p(x,y) be any point in the plane of directrix and focus, and mp be the perpendicular distance from p to the directrix,then p lies on parabola iff fp= mp.
(𝑥 − 9)² + 𝑦² = (𝑦 + 4)². The focus of a parabola is at (3, 6) and the directrix line is y = 4. Discover how to find the standard form of the parabola equation from the focus and directrix, as well as two other. 1 = 1 + p 2 2 = 1 + p p = 1.
The focus of a parabola is the fixed point located inside a parabola that is used in the formal definition of the curve.
Any point (𝑥, 𝑦) on the parabola is equidistant to the focus and the directrix. The focus of the parabola is f(3,0) and its directrix is the line x=−3 i.e., x+3=0. Hence equation is either y 2=4ax or y 2=−4ax. We can express these distances using the distance formula, and we get.
The four such possible orientations of the parabola are explained in the table below:
So, we have to use equation y 2=4ax. √ ( (𝑥 − 9)² + (𝑦 − 0)²) = √ ( (𝑥 − 𝑥)² + (𝑦 − (−4))²) simplifying and squaring both sides gives us. By using focus directrix property of parabola. Remember to balance the equation by adding the same constants to each side.
What is the equation of the parabola?
A parabola is defined as follows: Let s be a point and d be line. Equation of directrix is x = a. Now the focus has a positive x coordinate.