An ellipse is symmetric to both the coordinate axes. X,y are the coordinates of any point on the ellipse, a, b are the radius on the x and y axes respectively, ( * see radii notes below ) t is the parameter, which ranges from 0 to 2π radians. If the given coordinates of the vertices and foci have the form (±a,0) ( ± a, 0).
Find the center, vertices, and foci of the ellipse with
Where, the major axis has a length of.
The equation of an ellipse that has its center at the origin, (0, 0), and in which its major axis is parallel to the x axis is:
1 − ( x a) 2. Learn what the standard form of an ellipse equation is, how to identity the center and size of the. The required equation of ellipse is \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) \(\dfrac{x^2}{16} + \dfrac{y^2}{12} = 1\) therefore the required equation of the ellipse is \(\dfrac{x^2}{16} + \dfrac{y^2}{12} = 1\). Then the ellipse is a circle.
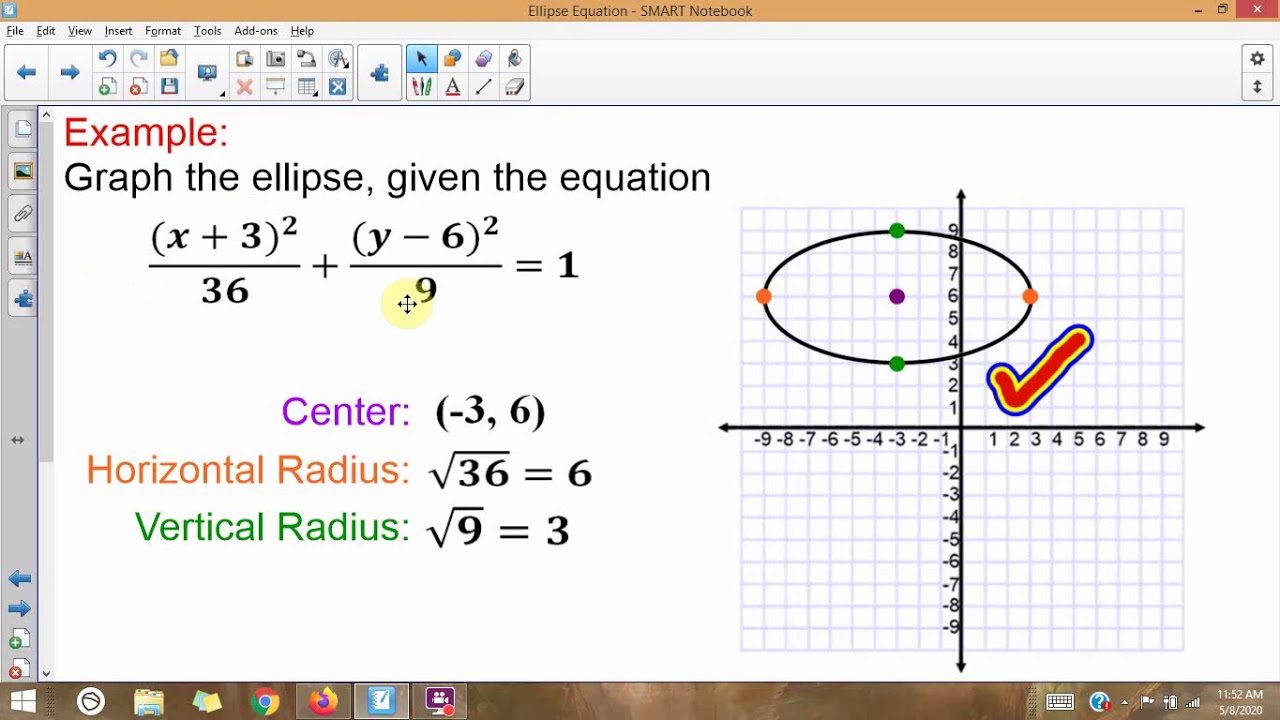
General equation of an ellipse (x h)2 a2 + (y k)2 b2 = 1 center at (h;k) vertices at (h +a;k), (h a;k), (h;k +b), (h;k b) university of minnesota general equation of an ellipse
The equation that defines an ellipse of the type shown in figure 7 is: (center at x = 0 y = 0) the eccentricity e of an ellipse: Given the vertices and foci of an ellipse centered at the origin, write its equation in standard form. The general equation of an ellipse centered at (h,k) ( h, k) is:
The vertices are located at the points.
(h, k) is the center point, a is the distance from the center to the end of the major axis, and b is the distance from the center to the end of the minor axis. Since a = b in the ellipse below, this ellipse is actually a circle whose standard form equation is x² + y² = 9 graph of ellipse from the equation the problems below provide practice creating the graph of an ellipse from the equation of the ellipse. (x−h)2 a2 + (y−k)2 b2 =1 ( x − h) 2 a 2 + ( y − k) 2 b 2 = 1. The ellipse equation in standard form involves the location of the ellipse's center and its size.
Area of an ellipse proof.
The covertices are located at the points. To write the equation of an ellipse, we must first identify the key information from the graph then substitute it into the pattern. {eq}\frac {x^2} {a^2} + \frac {y^2} {b^2} = 1 {/eq} where: We know the general equation for an ellipse is x2 a2 + y2 b2 = 1 x 2 a 2 + y 2 b 2 = 1.
X 2 /b 2 + y 2 /a 2 = 1.
As we can see the ellipse is divided into four quadrants. In general, an ellipse may be centered at any point, or have axes not parallel to the coordinate axes. 1 2 2 2 2 + = b y a x the curve is described by two lengths, a and b. ( 10 , 0 ) , ( −10 , 0 )
The minor axis has a length of.
Then the ellipse is a hyperbola. X 2 /a 2 + y 2 /b 2 = 1. Then it is an ellipse. General equation of an ellipse the standard equation for an ellipse, x 2 / a 2 + y 2 / b 2 = 1 , represents an ellipse centered at the origin and with axes lying along the coordinate axes.
Then the ellipse is a parabola.
Writing the equation of an ellipse. Writing equations of ellipses date_____ period____ use the information provided to write the standard form equation of each ellipse. K), (i) for ellipse a > b, the equation of directrix is x = a e + h and x = − a e + h. (ii) for ellipse a < b, the equation of directrix is y = b e + k and y = − b e + k.
So calculating the area of 1 quadrant and multiplying by 4, we get the area of an ellipse.
Y = b.√1−(x a)2 y = b. Ellipses not centered at the origin. In polar coordinates, with the origin at the center of the ellipse and with the angular coordinate measured from the major axis, the ellipse's equation is: Remember the patterns for an ellipse:
X = a cos ty = b sin t.
An ellipse is one of the shapes called conic sections, which is formed by the intersection of a plane with a right circular cone. An ellipse is a two dimensional closed curve that satisfies the equation: The general equation of an ellipse whose focus is (h, k) and the directrix is the line ax + by + c = 0 and the eccentricity will be e is sp = epm. Just as with the circle equations, we subtract offsets from the x and y terms to translate (or move) the ellipse back to the origin.