Conic sections examples solutions s activities. For a hyperbola, there are two foci $a,b$, and the absolute value of the difference of the distances to both foci is constant. Why is the diffeial equation of ellipse and hyperbola same quora.
Conic Sections (Circle, Parabola, Ellipse, and Hyperbola
#aneb# but a and b both have different signs.
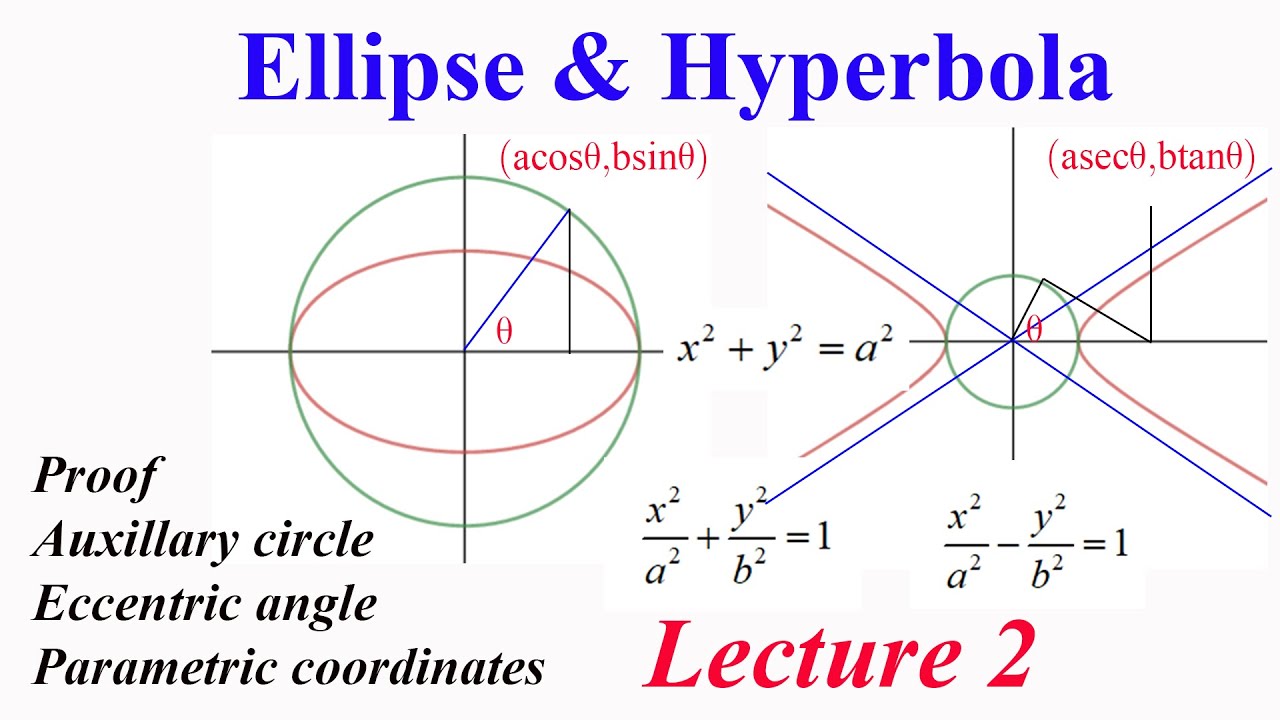
There are two given points, the foci, aellipse is the locus of points such that the sum between the distances to each focus is constant.the standard equation.
Free conic section posters covering circle ellipse hyperbola parabola properties check it out today math homework help ellipses The vertex of the parabola. Identify the equation as a parabola, circle, ellipse, or hyperbola : In this equation, y2 is there, so the coefficient of x.
Either a or b equals 0 (only one squared term in the equation).
So, in the problem stated above, since #aneb# (#4ne9#),. Difference between parabola and hyperbola v s. Is the curve a parabola or ellipse or hyperbola? Or 2x + 5y = 100
Using all standard equations, the length of latus rectum:
This video tutorial shows you how to graph conic sections such as circles, ellipses, parabolas, and hyperbolas and how to write it in standard form by comple. Parabolas hyperbolas ellipses and circles. How to do conic sections wikihow. Write the equation of an ellipse, hyperbola, parabola in complex form.
It includes parabola, ellipse, hyperbola and circle.
Conics ellipse hyperbola parabola circle. For hyperbola = \(2 \frac{b^2}{a}\) Learn how to classify conics easily from their equation in this free math video tutorial by mario's math tutoring. 3.5 parabolas, ellipses, and hyperbolas to summarize:
This type of the equation is useful, since you’ll be able to simply discover the middle and the radius.
Parametric equation of a parabolathe Their equation contains xterms,yterms x t e r m s, y t e r m s, or both. If e=1, the conic is a parabola; Define b by the equations c 2 = a 2 − b 2 for an ellipse and c 2 = a 2 + b 2 for a hyperbola.
Which way does the parabola open?
For parabola = \(4a\) 4. A plane is cutting through a cone. And if e>1, it is a hyperbola; Then read off a and b.
We know that, if $e$ is the eccentricity of the ellipse, then distance between foci is $2ae$.
We discuss ellipses, hyperbolas, circles. If eccentricity, e = 0, the conic is a circle; For ellipse = \(2 \frac{b^2}{a}\) 2. Choose the one alternative that best completes the statement or answers the question.
L equation d une ellipse.
Here h = k = 0. Find the center by completing squares. For a circle, c = 0 so a 2 = b 2. For circle = \(2r\) 3.
For an ellipse, there are two foci $a,b$, and the sum of the distances to both foci is constant.
The general equation ax2 + bxy + cy2 + dx + ey + f = 0 this equation is of second degree, containing any and all of 1, x, y, x2, xy, y2. Conics ellipse hyperbola parabola circle. Sample questions based on conic sections: The focus and the directrix solution to problem 2 opens up vertex:
Here is how you distinguish the various conic sections from the coefficients in the general equation:
Therefore, the equation of the circle is. Let us start with the conics’ introduction of circles, eclipses, parabolas, and hyperbolas which includes the set of curves formed by the intersection of. If 0, the conic is an ellipse; Conic sections types properties and examples.
The centre of the ellipse is $c\left( \frac{{{z}_{1}}+{{z}_{2}}}{2} \right)$ length of the major axis of the ellipse is $2a$.
Conic sections circles ellipses parabolas hyperbola how to graph write in standard form you.