The area of an ellipse is: (4 √6 / 5 , 2/5) shown below is the graph of a circle and an ellipse and their points of intersection. An ellipse is a conic section, formed by the intersection of a plane with a right circular cone.
Ellipse and Hyperbola Mathematics Notes for IITJEE Main
‘r’ is the radius of the circle.
Distance between the centre and either focus is c with c 2 =h 2 −k 2, h>k>0:
Area of the circle is calculated based on its radius, but the area of the ellipse depends on the length of the minor axis and major axis. Circle has one radius, which lies at the center. Where ‘r’ is the radius of the circle. Ellipse centered at the origin.
A circle is an ellipse, with a condition where both foci/focus are at the same point (i.e.
University of minnesota general equation of an ellipse. = 1 the unit circle is stretched r times wider and r times taller. Π × a × b. Π × a × b.
Now lets graph the ellipse x2 16 + y2 36 = 1 15.
The vertex of the parabola is at (h, k). The right side of the equation is 1. Circle (x−a) 2 +(y−b) 2 =r 2: This is a circle, and you will get an equation that looks like where r is whatever radius you set up.
Therefore, by substituting a and b by r;
From the equation to find the radius you take the square root of r2. For a circle, a and b are equal to the radius, and you get π ×. The coordinates of the vertices are (±a,0) ( ± a, 0) the length of the minor axis is 2b 2 b. Parabolas a parabola is a curve that is oriented either up, down, left, or right.
If the ellipse is oriented horizontally, and:
A and b are from the center outwards (not all the way across). This equation is in standard form. Here h = k = 0. Therefore, the equation of the circle is.
The standard form for the equation of the ellipse is:
The ellipse equation in standard form involves the location of the ellipse's center and its size. The length of the major axis is 2a 2 a. If the ellipse \frac {x^2}{a^2} + \frac {y^2}{b^2} =1 is to enclose the circle x^2 + y^2 = 2y, what values of a and b minimize the area of the ellipse? Equation of ellipse in parametric form.
The points of intersection of the ellipse and the circle are.
Center is (a,b) radius is r: Ellipse with the horizontal major axis (x−a) 2 /h 2 +(y−b) 2 /k 2 =1: Area of the circle = πr 2. We get the standard equation of a circle with radius r and the center (h, k):
Find the coordinates of the focus, axis, the equation of the directrix and latus rectum of the parabola y2 = 16x.
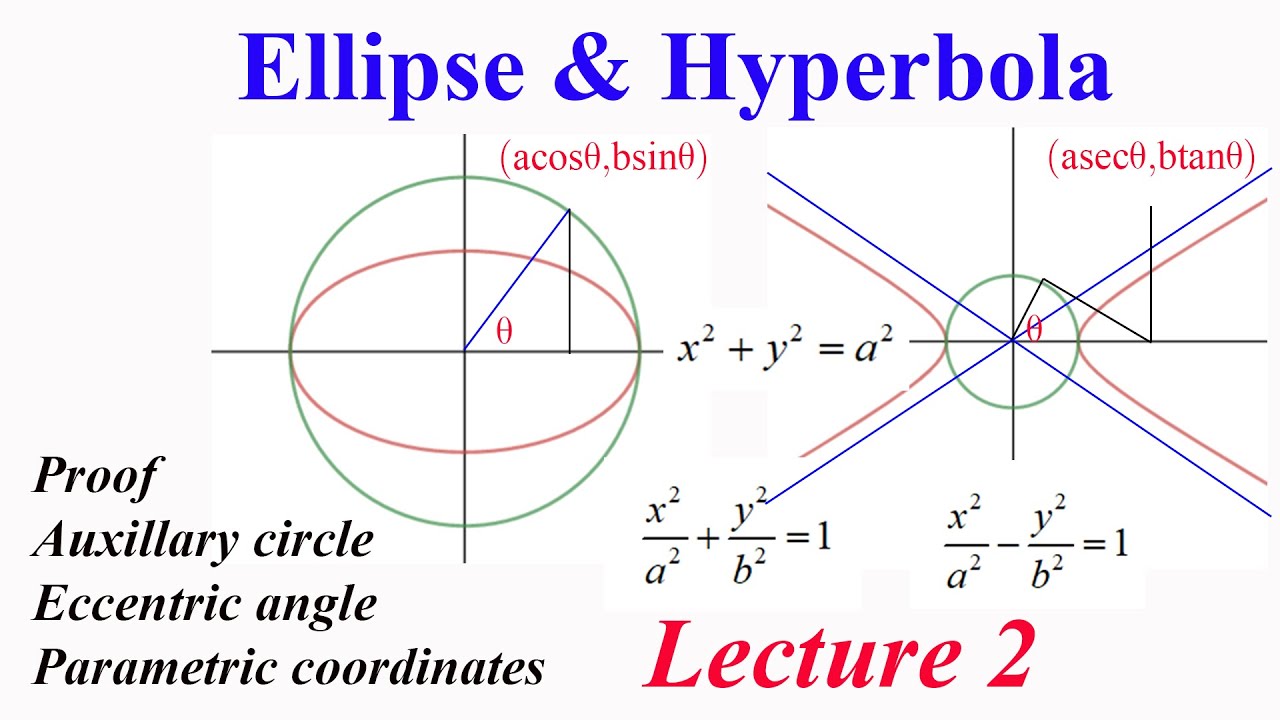
The circle is a special case of the ellipse where a=b=r, in the equation of the ellipse. Learn what the standard form of an ellipse equation is, how to identity the center and size of the. Length of the minor axis is 2k. Referring to the standard equation of the ellipse, x 2 a 2 + y 2 b 2 = 1, choose the centre of the circle to correspond to the parameter value θ, so the equation of the circle with this centre and radius r is (x − a cos θ) 2 + (y − b sin θ) 2 = r 2.
In this equation, y2 is there, so the coefficient of x.
Note that when a = b then f = 0 it means that the ellipse is a circle. In the applet above, click 'reset' and drag the right orange dot left until the two radii are the same. The flattening f of an ellipse is the amount of the compression of a circle along a diameter to: This demonstrates that a circle is just a special case of an ellipse.
The distance from the center to any point on the line is called the radius of the circle.
Since a = b in the ellipse below, this ellipse is actually a circle whose standard form equation is x² + y² = 9 graph of ellipse from the equation the problems below provide practice creating the graph of an ellipse from the equation of the ellipse. X2 a2 + y2 b2 =1 x 2 a 2 + y 2 b 2 = 1. Center is (a, b) length of the major axis is 2h. The parametric equation of an ellipse :
= 1 the unit circle is stretched a times wider and b times taller.
Ellipse with the vertical major axis (x−a) 2 /k 2 +(y−b) 2 /h 2 =1: A >b a > b. Ellipse has two foci, which are at the either ends. (x−h)2 a2 + (y−k)2 b2 =1 ( x − h) 2 a 2 + ( y − k) 2 b 2 = 1.
A circle is just a particular ellipse.
Form an ellipse and its value is: