B = − 1 5. We will choose ( − 5, 10) as point one and ( − 3, 4) as point two. Let p 1 (x 1, y 1) and p 2 (x 2, y 2) be the two given points on the line l.
Slope Formula Finding Slope of a Line Given Two Points
We've got a value for m and a value for b.
That means, slope of p 1 p = slope of p 1 p 2.
A line passing through the given two points. Plug the slope and the x and y of one of the given points into y = mx + b, then. Choose two points that are on the line. What is the example of a two point form?
The apostrophe is used to denote the other point, different from point (x,y).
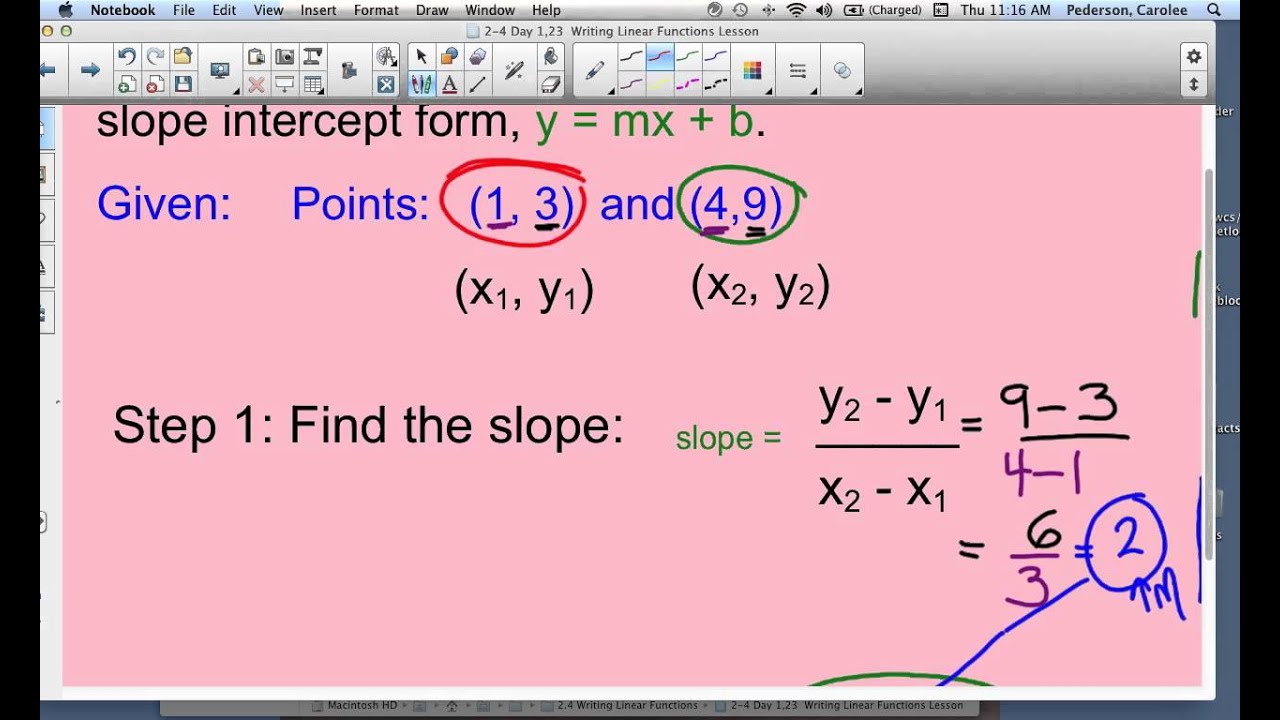
1 ©y t2u0k1t7z kkjuotvac ws_osfnt_waatrieq slrlccv.a x gaolplb lrniqgbhxtpss `rre`svearkvlebdv. Y = mx + c. (it does not matter which is point one and which is point two as long as we stay consistent throughout our calculations.) Slope = m = rise run = y 2 − y 1 x 2 − x 1.
How do you find the y intercept with.
Two point form of the equation of a line. Slope is the coefficient of x. This is the graph of the line showing that it passes both of the two points. Your goal is to get the equation into slope intercept format y = mx + b.
We need to find slope a and intercept b.
By using this website, you agree to our cookie policy. We can write an equation of the line that passes through the points y=0 as follows: Find the slope using the slope formula. Here's a simple step by step guide on how to work out the equation in slope intercept form (y = mx + b) for example, given the two points (1,5) and (3,1), let's work out the solution.
M = y 2 − y 1 x 2 − x 1 = ( − 1) − 3 3 − ( − 3) = − 4 6 = − 2 3.
Y = mx + b calculate the slope, m, from the given point values, solve for b by using one of the point values, and check your solution using the other point values. Two points the slope and one point. Write the equation in slope intercept form. If the coordinates of two points are known to us, then we can find the slope of the line that will pass through these points by dividing the change.
Thus, for any two points defined by cartesian (planar) coordinates such as those given in this problem,.
Remember, the slope is equal to the change in y divided by the change in x (rise over run). Use one of the points as (x,y) to solve for b. From the figure, we can say that the three points p 1, p 2 and p are collinear. Y = mx + b.
Let p (x, y) be a general point on the line l.
Once you have the slope, m for the equation y = mx + b ; For two known points we have two equations in respect to a and b. Calculate the slope between the two points. Let's subtract the first from the second and from there.
Y = mx + b.
Note that b can be expressed like this Find the slope using the formula: A line can be thought of as the ratio of the change between horizontal (x) and vertical (y) positions. Lets call the (1,5) point 1 and (3,1) point 2 for reference.
We have two points, ( − 5, 10) and ( − 3, 4).
The coordinates in this level of printable worksheets are given in the form of fractions. Add 2y to both sides to get 6x = 12 + 2y; The equation of slope intercept varies in usa and uk. Where, x, y represents the x and y coordinates, m is slope of line, and.
This gives us the linear function.
Let's quickly review the steps for writing an equation given two points: Slope intercept form is :