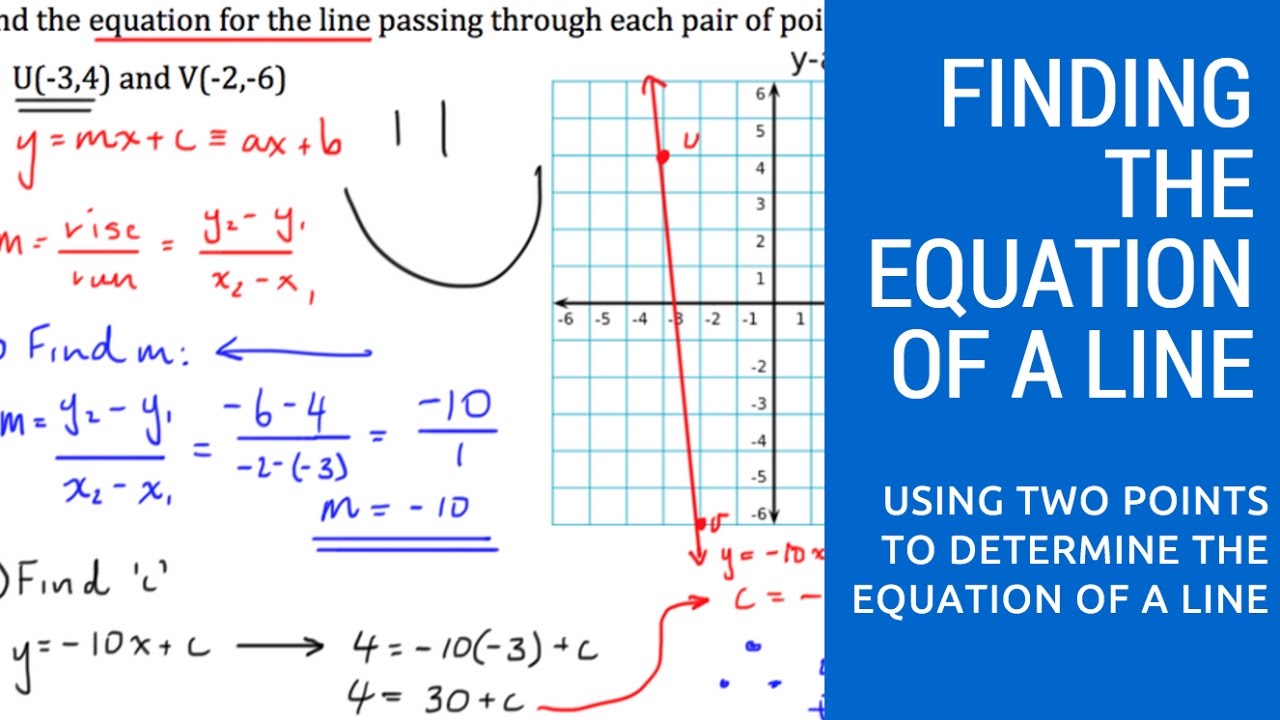
Find the equation of line passes through the point. (iv) the graph of the equation y = a is a straight. M = change in y change in x = 4−3 6−2 = 1 4.
Linear Equation Through Two Points YouTube
Y − y 1 = m ( x − x 1) y − y 1 = 2 ( x − x 1) step 3.
The formula to find equation of straight line with two points is:
By using this website, you agree to our cookie policy. For two known points we have two equations in respect to a and b. Q = ( − 3, 0, 1). Find the equation of a line through the points ( 3, 7) and ( 5, 11).
This assignment is perfect for the month of december, the holiday season or christmas!
We will use the first point. Substitute the slope for 'm' in the point slope equation. Steps to find the equation of a line from two points: Students will practice using two points to cre.
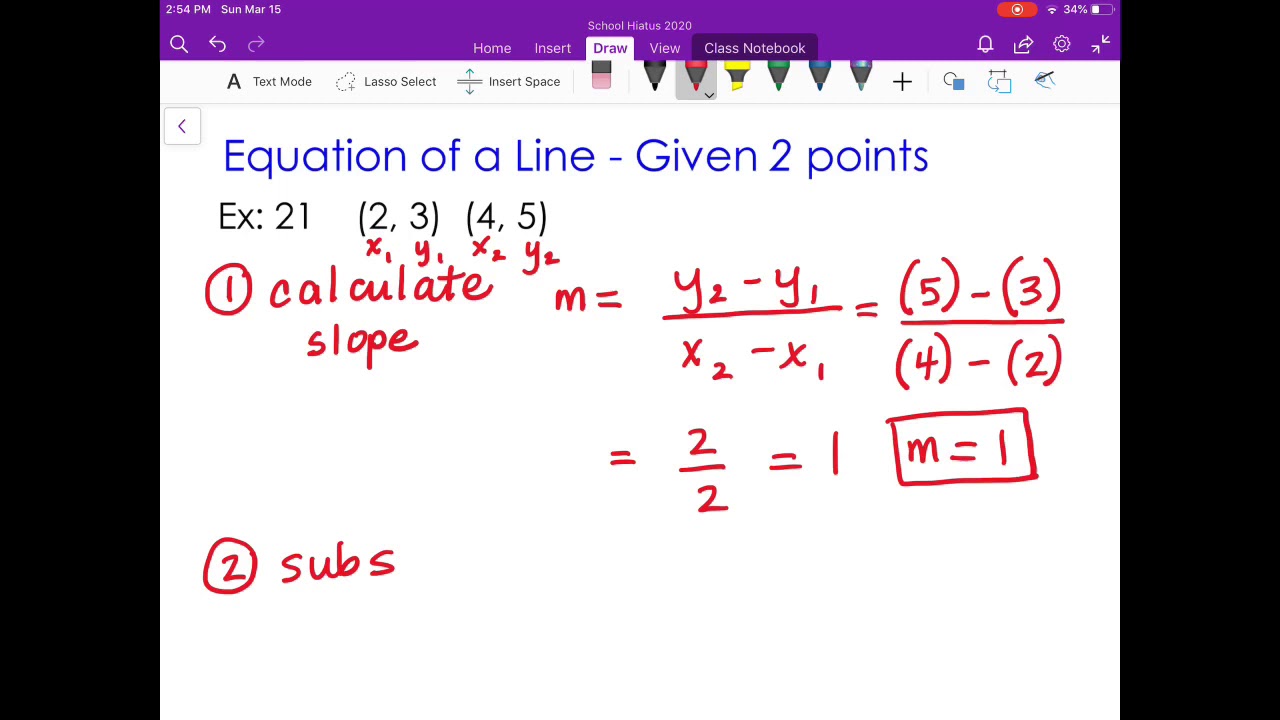
Calculate the slope from the 2 points.
Let's subtract the first from the second and from there. Y − 3 = 1 4 (x − 2) that is an answer, but we can simplify it further. Two point form of a line. Build your own widget » browse widget gallery » learn more » report a problem » powered by wolfram|alpha.
Y − y1 = m (x − x1) we can choose any point on the line for x1 and y1, so let's just use point (2,3):
Just type numbers into the boxes below and the calculator will automatically calculate the equation of line in standard, point slope and slope intercept forms. Slope y 2 − y 1 x 2 − x 1 11 − 7 5 − 3 4 2 = 2. If we have any two points on the line, we can use this formula to find the equation. First, calculate the slope, , for any two points.
Equation of line from 2 points calculator.
Let (x 1, y 1) and (x 2, y 2) be the two points such that the equation of line passing through these two points is given by the formula: Note that b can be expressed like this We need to find slope a and intercept b. Equation of a line using two points on the line :
Y − 3 = m (x − 2) we already calculated the slope m:
Equation of a straight line can also be evaluated with one point and slope using our point slope form calculator. To find equation of the line passing through points $a(x_a, y_a)$ and $b(x_b, y_b)$ ( $ x_a \ne x_b $), we use formula: The slope of the line joining two points (x. How to find equation of the line determined by two points?
The formula of two point form of a equation is given below:
It calculates the point slope form equation by using 2 points of a straight line. From numpy import ones,vstack from numpy.linalg import lstsq import math points = [ (30, 220), (1385, 1050)] x_coords, y_coords = zip (*points) a = vstack ( [x_coords,ones (len (x_coords))]).t m, c = lstsq (a, y_coords) [0] print (line solution is y = {m}x + {c}.format (m=m,c=c)) show activity on this post. Enter any number into this free calculator. Slope = y 2 − y 1 x 2 − x 1.
Let m be the slope of line passing through ( x 1, y 1) and ( x 2, y 2).
(i) the graph of a linear equation in two variables is a straight line. We will use the first two. The equation of a line passing through two points ( x 1, y 1) and ( x 2, y 2) is. Graphical representation of linear equation in two variables:
Y −y1 = y2−y1 x2−x1 (x.