(x 2)2 + (y− 6)2 = 72 standard form of the equation of a circle (x h)2 + (y− k)2 = r2 this is with h = 2. R=square root of 7 ; The center is (h,k) and the radius measures r units.
Ex 4 Write General Equation of a Circle in Standard Form
Up to 24% cash back example 2.
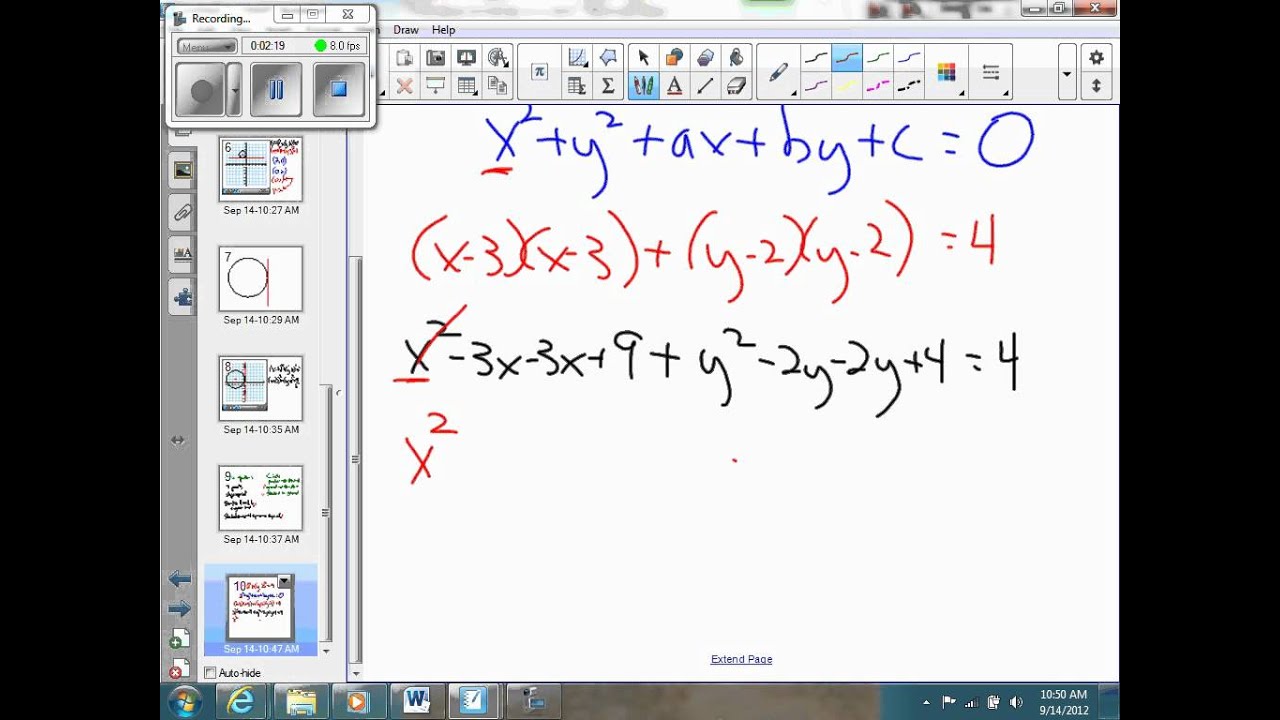
X 2 + y 2 + c x + d y + e = 0 here c , d , and e are real numbers.
The center is (h,k) and the radius measures r units. And that is the standard form for the equation of a circle! X 2 + y 2 + 2gx + 2fy + c = 0. Write in standard form and graph:
It shows all the important information at a glance:
Center = ⎛ ⎜⎝ h −3, k −4 ⎞ ⎟⎠, radius = r 3. Adding g2 + f2 on both sides of the equation. To graphically represent a circle equation, first discover the coordinates of the center of the circle and the radius of the circle using the circle equation. A circle's equation can have either a general or standard form.
X 2 + y 2 + 2gx + 2fy + c = 0.
H, k is defined as the center coordinates. We are then told that circle a will be moved by five units and then left by six units. Parametric form equation of a circle The general form of the equation of circle is:
From this circle equation, you can easily tell the coordinates of the center and the radius of the circle.
Convert the equation of a circle in general form below to standard form. Where r is defined as the radius of the circle. ( x − 9) 2 + ( y − 6) 2 = 100 is a circle centered at (9, 6) with a radius of 10. Center = (h,k), radius = r.
(x − 9) 2 + (y − 7) 2 = 25 c:
The standard equation of a circle with the center at and radius is you can convert general form to standard form using the technique known as completing the square. (x −h)2 + (y −k)2 = r2; / best coding standards javascript / under :algae biofuel google scholar. So, substituting these values into (i), we get:
X2 + y2 + 2gx + 2fy + c + g2 + f2 = g2 + f2.
The center (a,b) and the radius r. X2 + y2 + 2gx + 2fy + c = 0. Write the standard form of the equation and the general form of the equation of the circle of radius r and center (h,k). (x−a) 2 + (y−b) 2 = r 2.
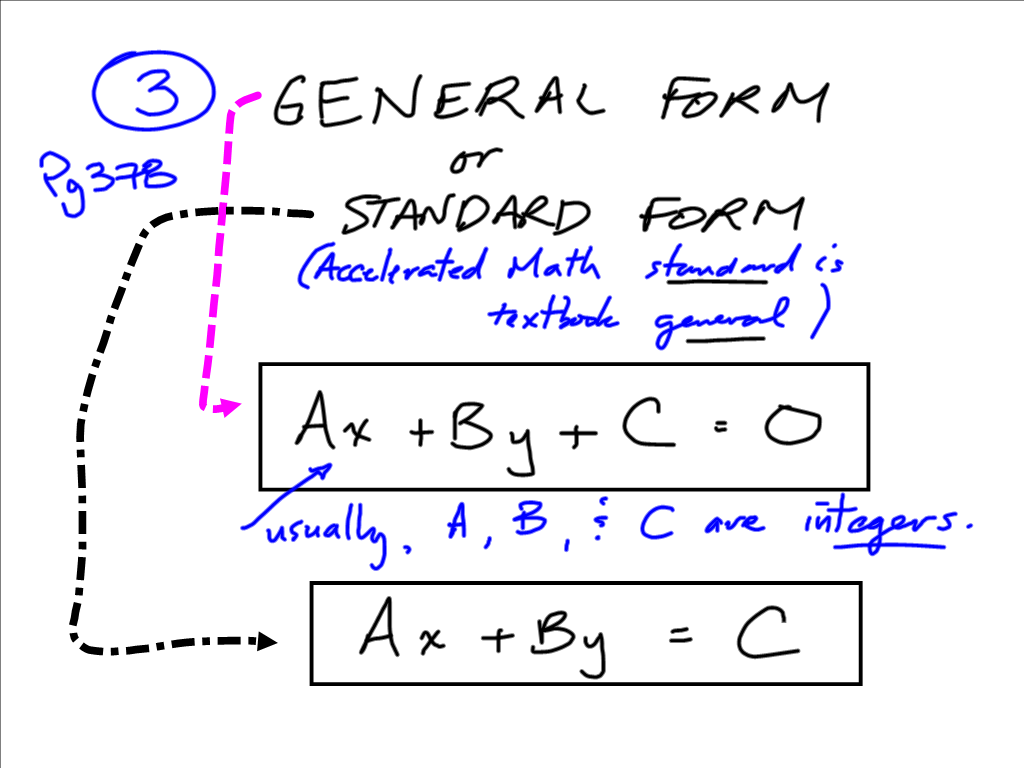
The general equation of any type of circle is represented by:
Here, we will take an example that gives us an idea to transform an equation from a standard form to a general form This general form is used to find the coordinates of the center of the circle and the radius of the circle. Where r is defined as the radius of the circle. (x + 9) 2 + (y + 7) 2 = 25.
Standard form to general form.
Equation of a circle with centre (h, k) and radius r : Recall that the formula for the equation of a circle in standard form is: We cannot use (x, y) ( x, y) for all the graph points, so we use other letters to identify the coordinates of the center of the circle, in this case (a, b) ( a, b): H and k are the x and y coordinates of the center of the circle.
The standard form of a circle is that expression we just derived from the pythagorean theorem!
(x − 2)2 + (y − 6)2 = 49 Find the center and radius of the circle having the equation: (x−h)2 this is with k = 6. Is a way to express the definition of a circle on the coordinate plane.
The graph is shown below.
Firstly, we will transform the standard form to the general form. R2 we use the center, (h, k) = (2, 6), and the radius, r = 7, to graph the circle. Experts are tested by chegg as specialists in their subject area. The formula is ( x − h) 2 + ( y − k) 2 = r 2.
Find the general shape of the equation of a circle centered at (−3.5) and through (1,−2).
Standard form to general form. We review their content and use your feedback to keep the quality high. X2 + y2 + 18x + 14y + 105 = 0 a: Here, c is a constant term, and the equation having c value represents a.
General form of the equation of a circle :
Standard form equation of a circle. Equation of a circle in standard formrecruitment statement. Standard form for the equation of a circle is (x−h)2+(y−k)2=r2. To graph a circle mark points r units up, down, left, and right from the center.
H, k is defined as the center coordinates.
To the left of six units. Convert the equation of a circle in general form below to standard form. The standard form is simpler to understand when compared with the general form of the equation of a circle. For the circle we are given, we have:
(x + 9) 2 + (y + 7) 2 = 5 b:
Firstly, we will transform the standard form to the general form. It is the same idea as before, but we need to subtract a and b: Write the standard form of the equation and the general form of the equation of the circle of radius r and center (h,k). (y−k)2 this is with r = 7.